题目内容
6.下列命题中:①若A∈α,B∈α,C∈AB,则C∈α;
②若α∩β=l,b?α,c?β,b∩c=A,则A∈l;
③A,B,C∈α,A,B,C∈β且A,B,C不共线,则α与β重合;
④任意三点不共线的四点必共面.
其中真命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用平面的基本性质对四个命题分别分析解答.
解答 解:对于①,若A∈α,B∈α,C∈AB,根据平面的基本性质得到C∈α;故意正确;
对于②,若α∩β=l,b?α,c?β,b∩c=A,根据平面的基本性质容易得到A同时在两个平面内,即A∈l;故②正确;
对于③,A,B,C∈α,A,B,C∈β且A,B,C不共线,根据不共线的三点确定一个平面,容易得到α与β重合;故③正确;
对于④,任意三点不共线的四点不一定共面.比如空间四面体;故④错误;
故选D.
点评 本题考查了平面的基本性质的运用;熟练掌握平面的性质是关键.

练习册系列答案
相关题目
19.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,且|$\overrightarrow{b}$|=2,$\overrightarrow{b}$$•(2\overrightarrow{a}-\overrightarrow{b})$=0,则|$\overrightarrow{a}$|的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
14.已知命题p:若a>b,则a2>b2;q:“x≤1”是“x2+2x-3≤0”的必要不充分条件.则下列命题是真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
15.已知一几何体的三视图如图所示,则该几何体的体积是( )
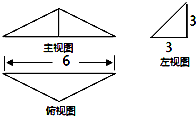

| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
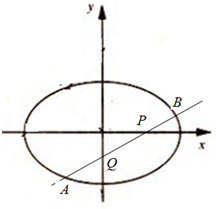 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.