题目内容
【题目】（已知函数f（x）=|2x+1|+|x﹣2|，不等式f（x）≤2的解集为M．
（1）求M；
（2）记集合M的最大元素为m，若正数a，b，c满足abc=m， 求证： 
．
【答案】
（1）解：f（x）=|2x+1|﹣|x﹣2|≤2化为：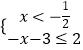 
或 
或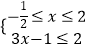 
或 
所以集合M={x|﹣5≤x≤1}
（2）解：集合M中最大元素为m=1，所以abc=1，其中a＞0，b＞0，c＞0
因为 
， 
，
，
三式相加得： 
，
所以 
【解析】（1）由零点分段法，分类讨论，即可求M；（2）abc=1，利用基本不等式，即可证明结论．
【考点精析】掌握不等式的证明是解答本题的根本，需要知道不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．
练习册系列答案
名校课堂系列答案
相关题目
