题目内容
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为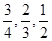 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.
(I)求随机变量 的分布列及其数学期望E
的分布列及其数学期望E ;
;
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
(Ⅰ)分布列见解析,期望为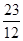 ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)先分析 的所有可能取值,再分析
的所有可能取值,再分析 取每一个可能值时每个人的答题情况,将若干个简单互斥事件的和,再分析每个简单事件的中每个人的答题情况,将其表示成若干个相互独立事件的积,再用互斥事件的积概率公式和相互独立事件的和概率公式,求出
取每一个可能值时每个人的答题情况,将若干个简单互斥事件的和,再分析每个简单事件的中每个人的答题情况,将其表示成若干个相互独立事件的积,再用互斥事件的积概率公式和相互独立事件的和概率公式,求出 每种取值情况的概率,列出分布列,再代入期望公式求出
每种取值情况的概率,列出分布列,再代入期望公式求出 的期望;(Ⅱ)先分析甲乙两队分数之和为4的甲乙两队的得分情况,将其分成若干个互斥事件的和,再根据每个互斥事件甲乙的两队的得分情况,化为相互独立事件的积,利用互斥事件的和概率公式和相互独立事件的积概率公式求出甲乙两队的分值和为4的概率,在计算出甲队比乙队得分高的概率,利用条件概率公式即可所求事件的概率.
的期望;(Ⅱ)先分析甲乙两队分数之和为4的甲乙两队的得分情况,将其分成若干个互斥事件的和,再根据每个互斥事件甲乙的两队的得分情况,化为相互独立事件的积,利用互斥事件的和概率公式和相互独立事件的积概率公式求出甲乙两队的分值和为4的概率,在计算出甲队比乙队得分高的概率,利用条件概率公式即可所求事件的概率.
试题解析:(1) 的可能取值为0,1,2,3
的可能取值为0,1,2,3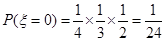 ;
;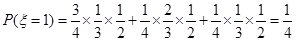 ;
;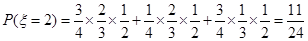 ;
;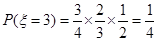 4分
4分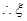 的分布列为
的分布列为
0 1 2 3 
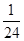

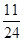

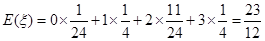 6分
6分
(2)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B
则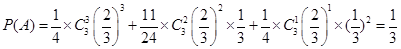 ; 8分
; 8分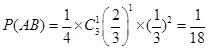 10分
10分
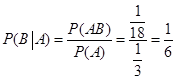 12分
12分
考点:随机变量分布列与期望,互斥事件的概率计算,相互独立事件概率,独立重复试验,条件概率,应用意识

练习册系列答案
相关题目
某工厂生产A,B两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下:
| 测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产1个元件A,若是正品则盈利40元,若是次品则亏损5元;生产1个元件B,若是正品则盈利50元,若是次品则亏损10元.在(1)的前提下,
(ⅰ)X为生产1个元件A和1个元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5个元件B所得利润不少于140元的概率.
 ,乙胜的概率为
,乙胜的概率为 ,且每局比赛胜负互不受影响.
,且每局比赛胜负互不受影响. 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 的概率;
的概率;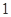 个点,连续取
个点,连续取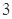 次,得到
次,得到 ,求
,求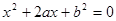 是关于
是关于 的一元二次方程.
的一元二次方程.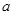 是从集合
是从集合 四个数中任取的一个数,
四个数中任取的一个数,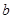 是从集合
是从集合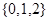 三个数中任取的一个数,求上述方程有实数根的概率;
三个数中任取的一个数,求上述方程有实数根的概率; ,
, ,求上述方程有实数根的概率.
,求上述方程有实数根的概率.