题目内容
15.下列三函数中,与sin$\frac{π}{3}$数值相同的是( )①sin(nπ+$\frac{4}{3}$π)
②cos(2nπ+$\frac{π}{6}$);
③sin(2nπ+$\frac{π}{3}$);
④cos[(2n+1)π-$\frac{π}{6}$];
⑤sin[(2n+1)π-$\frac{π}{3}$](n∈Z).
| A. | ①② | B. | ①③④ | C. | ②③⑤ | D. | ①⑤ |
分析 直接利用诱导公式以及三角函数求值,判断即可.
解答 解:①sin(nπ+$\frac{4}{3}$π)=±$\frac{\sqrt{3}}{2}$.
②cos(2nπ+$\frac{π}{6}$)=$\frac{1}{2}$;
③sin(2nπ+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$;
④cos[(2n+1)π-$\frac{π}{6}$]=$\frac{1}{2}$;
⑤sin[(2n+1)π-$\frac{π}{3}$]=$\frac{\sqrt{3}}{2}$(n∈Z).
与sin$\frac{π}{3}$数值相同的是①⑤.
故选:D.
点评 本题考查三角函数值的求法,诱导公式的应用,基本知识的考查.

练习册系列答案
相关题目
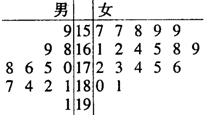 2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.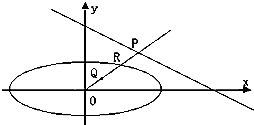 已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.
已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1. 如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.
如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.