题目内容
19.实数a、b、c满足a2+b2+c2=5.则6ab-8bc+7c2的最大值为45.分析 将a2+b2+c2分拆为a2+($\frac{1}{9}$+$\frac{8}{9}$)b2+($\frac{2}{9}$+$\frac{7}{9}$)c2 是解决本题的关键,再运用基本不等式a2+b2≥2ab求最值.
解答 解:因为5=a2+b2+c2=a2+($\frac{1}{9}$+$\frac{8}{9}$)b2+($\frac{2}{9}$+$\frac{7}{9}$)c2
=(a2+$\frac{1}{9}$b2)+($\frac{8}{9}$b2+$\frac{2}{9}$c2)+$\frac{7}{9}$c2
≥$\frac{2}{3}$|ab|+$\frac{8}{9}$|bc|+$\frac{7}{9}$c2
≥$\frac{2}{3}$ab-$\frac{8}{9}$bc+$\frac{7}{9}$c2
=$\frac{1}{9}$[6ab-8bc+7c2],
所以,6ab-8bc+7c2≤9×5=45,
即6ab-8bc+7c2的最大值为45,当且仅当:a2=$\frac{1}{9}$b2,$\frac{8}{9}$b2=$\frac{2}{9}$c2,
解得,a2=$\frac{5}{46}$,b2=$\frac{45}{46}$,c2=$\frac{180}{46}$,且它们的符号分别为:a>0,b>0,c<0或a<0,b<0,c>0.
故答案为:45.
点评 本题主要考查了基本不等式在求最值问题中的应用,以及基本不等式取等条件的确定,充分考查了等价转化思想与合理分拆的运算技巧,属于难题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
9.若sinα+sinβ=1-$\frac{\sqrt{3}}{2}$,cosα+cosβ=$\frac{1}{2}$.则cos(α-β)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | 1 |
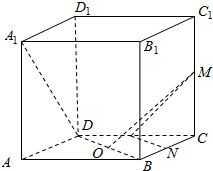 在单位正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、BC,CD的中点,O为底面ABCD的中心.
在单位正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、BC,CD的中点,O为底面ABCD的中心.