题目内容
9．若sinα+sinβ=1-$\frac{\sqrt{3}}{2}$，cosα+cosβ=$\frac{1}{2}$．则cos（α-β）的值为（ ）| A． | $\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{4}$ | D． | 1 |
分析 对sinα+sinβ=1-$\frac{\sqrt{3}}{2}$与cosα+cosβ=$\frac{1}{2}$等号两端分别平方后相加，即可求得答案．
解答 解：∵sinα+sinβ=1-$\frac{\sqrt{3}}{2}$①，
cosα+cosβ=$\frac{1}{2}$②，
∴①2+②2得：
sin2α+sin2β+2sinα•sinβ+cos2α+cos2β+2cosα•cosβ=（1-$\frac{\sqrt{3}}{2}$）2+（$\frac{1}{2}$）2，
即2+2cos（α-β）=1-$\sqrt{3}$+$\frac{3}{4}$+$\frac{1}{4}$，
∴cos（α-β）=-$\frac{\sqrt{3}}{2}$．
故选：B．
点评 本题考查两角差的余弦，考查同角三角函数间的关系，考查运算求解能力，属于中档题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
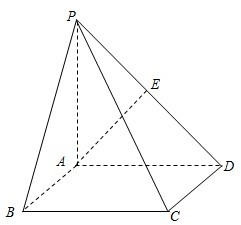在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是矩形，AE⊥PD于点E，l⊥平面PCD，求证：l∥AE．
1．
如图是函数f（x）=x3+bx2+cx+d的大致图象，则x1+x2等于（ ）
如图是函数f（x）=x3+bx2+cx+d的大致图象，则x1+x2等于（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | $\frac{12}{3}$ |