题目内容
7.已知函数f(x)=2x+b,g(x)=x2+bx+c,其中b、c∈R,设$h(x)=\frac{g(x)}{f(x)}$.(1)如果h(x)为奇函数,求实数b、c满足的条件;
(2)在(1)的条件下,若函数h(x)在区间[2,+∞)上为增函数,求c的取值范围;
(3)若对任意的x∈R恒有f(x)≤g(x)成立.证明:当x≥0时,g(x)≤(x+c)2成立.
分析 (1)根据函数奇偶性的定义建立方程关系进行求解即可.
(2)根据好是单调性的定义和性质建立不等式关系即可得到结论.
(3)根据条件求出c的取值范围,即可得到结论.
解答 解:(1)$h(x)=\frac{{{x^2}+bx+c}}{2x+b}$,设$h(x)=\frac{g(x)}{f(x)}$的定义域为D,
∵h(x)为奇函数,∴对于任意x∈D,h(-x)=-h(x)成立.…(1分)
即:$\frac{{{x^2}-bx+c}}{-2x+b}=-\frac{{{x^2}+bx+c}}{2x+b}$化简得:bx2-bc=0…(3分)
因对于任意x∈D都成立,
∴$\left\{{\begin{array}{l}{b=0}\\{bc=0}\end{array}}\right.$,
即b=0,c∈R…(4分)
(2)由(1)知b=0,∴$h(x)=\frac{1}{2}x+\frac{c}{2x}$…(5分)
∵h(x)在[2,+∞)上为增函数,
∴任取2≤x1<x2时,$f({x_2})-f({x_1})=\frac{1}{2}({x_2}-{x_1})(1-\frac{c}{{{x_1}{x_2}}})>0$恒成立.…(6分)
即任取2≤x1<x2时,1-$\frac{c}{{x}_{1}{x}_{2}}$>0成立,
也就是c<x1x2成立. …(8分)
∴c≤4,即c的取值范围是(-∞,4]. …(10分)
(3)因为任意的x∈R恒有f(x)≤g(x)成立,
所以对任意的x∈R,2x+b≤x2+bx+c,
即x2+(b-2)x+c-b≥0恒成立.…(11分)
所以判别式△=(b-2)2-4(c-b)≤0,
从而c≥$\frac{{b}^{2}+1}{4}$,
∴c≥1,且c$≥2\sqrt{\frac{{b}^{2}}{4}×1}$=|b|,…(13分)
因此 c(c-1)≥0且2c-b=c+(c-b)>0.…(14分)
故当x≥0时,有(x+c)2-g(x)=(2c-b)x+c(c-1)≥0.…(15分)
即当x≥0时,g(x)≤(x+c)2成立.…(16分)
点评 本题主要考查函数奇偶性的定义和单调性的应用,利用定义法是解决本题的关键.

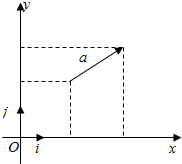 如图,在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量$\overrightarrow{i}$、$\overrightarrow{j}$作为基底.任作一个向量$\overrightarrow{a}$,由平面向量基本定理知,有且只有一对实数x、y,使得
如图,在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量$\overrightarrow{i}$、$\overrightarrow{j}$作为基底.任作一个向量$\overrightarrow{a}$,由平面向量基本定理知,有且只有一对实数x、y,使得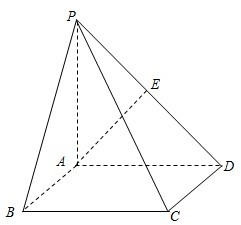 在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,AE⊥PD于点E,l⊥平面PCD,求证:l∥AE.
在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,AE⊥PD于点E,l⊥平面PCD,求证:l∥AE.