题目内容
在平面直角坐标系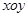 中,已知△
中,已知△ 顶点
顶点 (-4,0)和
(-4,0)和 (4,0),顶点
(4,0),顶点 在椭圆
在椭圆 上,则
上,则 = ( )
= ( )
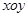 中,已知△
中,已知△ 顶点
顶点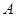 (-4,0)和
(-4,0)和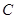 (4,0),顶点
(4,0),顶点 在椭圆
在椭圆 上,则
上,则 = ( )
= ( )A.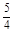 | B.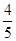 | C.1 | D.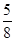 |
A
分析:由椭圆的性质得到A、C 是椭圆的两个焦点,由椭圆的定义知,AB+BC=2a=10,AC=8,
再利用正弦定理得
 =
= 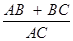 ,从而求出结果.
,从而求出结果.解:椭圆
 中.a=5,b=3,c=4,故A(-4,0)和C(4,0)是椭圆的两个焦点,
中.a=5,b=3,c=4,故A(-4,0)和C(4,0)是椭圆的两个焦点,∴AB+BC=2a=10,AC=8,由正弦定理得
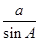 =
=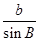 =
=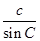 =2r,
=2r,∴
 =
=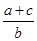 =
=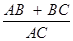 =
=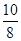 =
=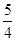 ,
,故选 A.

练习册系列答案
相关题目
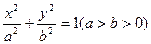 的长轴
的长轴 ,离心率
,离心率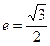 ,
, 为坐标原点,过
为坐标原点,过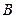 的直线
的直线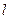 与
与 轴垂直,
轴垂直,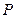 是椭圆上异于
是椭圆上异于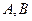 的任意一点,
的任意一点,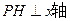 ,
,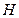 为垂足,延长
为垂足,延长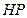 至
至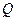 ,使得
,使得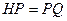 ,连接
,连接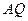 并延长交直线
并延长交直线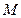 ,
,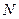 为
为 的中点
的中点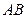 为直径的圆
为直径的圆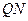 与圆
与圆
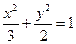 的左、右焦点分别为
的左、右焦点分别为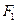 ,
,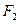 .过
.过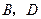 两点,过
两点,过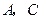 两点,且
两点,且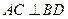 ,垂足为
,垂足为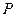 .
.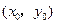 ,证明:
,证明: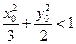 ;
; 的面积的最小值.
的面积的最小值.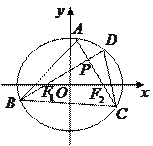
 过点(1,
过点(1, 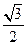 ),F1、F2分别为其左、右焦点,且离心率e=
),F1、F2分别为其左、右焦点,且离心率e=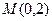 的直线
的直线 与椭圆C交于不同的两点
与椭圆C交于不同的两点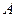 、
、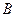 ,且∠
,且∠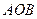 为锐角(其中
为锐角(其中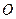 为坐标原点),求直线
为坐标原点),求直线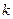 的取值范围.
的取值范围. 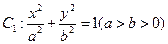 的左、右焦点分别为
的左、右焦点分别为 、
、 ,其中
,其中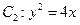 的焦点,
的焦点,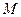 是
是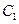 与
与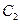 在第一象限的交点,且
在第一象限的交点,且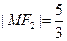 .
. 的顶点
的顶点 在椭圆
在椭圆 在直线
在直线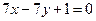 上,求直线
上,求直线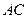 的方程.
的方程.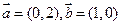 ,过定点
,过定点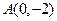 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点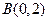 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
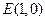 的直线
的直线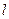 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求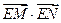 的取值范围
的取值范围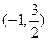 ;
;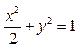 ,
,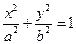
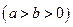 ,当
,当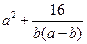 的最小值时,椭圆的离心率
的最小值时,椭圆的离心率 .
.