题目内容

19．若实数x、y满足约束条$\left\{\begin{array}{l}{3x-y-3≤0}\\{x-2y+4≥0}\\{2x+y-2≤0}\end{array}\right.$，则z=x+y的最大值为（　　）
A．1B．2C．3D．5

分析 先由约束条件画出可行域，再求出可行域各个角点的坐标，将坐标逐一代入目标函数，验证即得答案．

解答 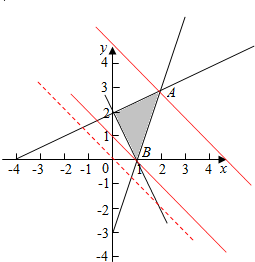解：如图即为满足不等式组$\left\{\begin{array}{l}3x-y-3≤0\\ x-2y+4≥0\\ 2x+y-2≤0\end{array}\right.$的可行域，
$\left\{\begin{array}{l}3x-y-3=0\\ x-2y+4=0\end{array}\right.$得A（2，3）．
由图易得：当x=2，y=3时
x+y有最大值5．
故选：D．

点评 在解决线性规划的小题时，常用“角点法”，其步骤为：①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证，求出最优解．

练习册系列答案
相关题目
17．已知向量$\overrightarrow{a}$=（cos$\frac{3x}{2}$，sin$\frac{3x}{2}$），$\overrightarrow{b}$=（cos$\frac{x}{2}$，-sin$\frac{x}{2}$），且x∈[0，$\frac{π}{2}$]．
（1）当x=$\frac{π}{2}$时，求|$\overrightarrow{a}-\overrightarrow{b}$|的值；
（2）若f（x）=$\overrightarrow{a}•\overrightarrow{b}$-2$λ|\overrightarrow{a}+\overrightarrow{b}|$的最小值是-$\frac{3}{2}$，求λ的值．
10．点（1，1）在不等式组$\left\{\begin{array}{l}{mx+ny≤2}\\{ny-mx≤2}\\{my≥1}\end{array}\right.$，表示的平面区域内，则m2+n2的取值范围是（　　）
A．[3，4]B．[2，4]C．[1，+∞）D．[1，3]
7．在△ABC中，B（4，0），C（-4，0）动点A满足sinB-sinC=$\frac{1}{2}$sinA则动点A的轨迹方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$（x＞2）．
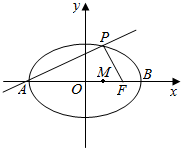14．如图所示，点A，B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于x轴上方，PA⊥PF，设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|．
（1）求点P的坐标；
（2）求点M的坐标；
（3）求椭圆上的点到点M的距离d的最小值．
4．函数y=$\frac{x}{\sqrt{-{x}^{2}-3x+4}}$的定义域为（　　）
A．（-∞，4）∪（1，+∞）B．（-4，1）C．（-4，0）∪（0，1）D．（-1，4）
11．已知数列{an}的前n项和Sn=$\frac{1}{2}$n2+$\frac{1}{2}$n，
（1）求数列{an}的通项公式；
（2）令bn=$\frac{1}{{a}_{n}{a}_{n+1}}$，求数列{bn}的前2015项和T2015．
8．在△ABC中，角A，B，C的对边分别为a，b，c，且$\frac{a}{sinA}=\frac{c}{{\sqrt{3}cosC}}$
（1）求角C的大小；
（2）如果a+b=6，$\overrightarrow{CA}•\overrightarrow{CB}=4$，求边长c的值．
9．a=0是复数a+bi（a，b∈R）为纯虚数的（　　）
A．必要条件B．充分条件
C．充要条件D．非充分非必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网