题目内容
7.在△ABC中,B(4,0),C(-4,0)动点A满足sinB-sinC=$\frac{1}{2}$sinA则动点A的轨迹方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$(x>2).分析 △ABC中,利用正弦定理,将sinB-sinC=$\frac{1}{2}$sinA转化为b-c=$\frac{1}{2}$a,再由双曲线的概念即可求其轨迹方程.
解答 解:∵B(4,0),C(-4,0)是△ABC 的两个顶点,内角A、B、C满足sinB-sinC=$\frac{1}{2}$sinA,
∴由正弦定理得b-c=$\frac{1}{2}$a,即|AC|-|AB|=$\frac{1}{2}$|BC|=4,
∴点A在以B(4,0),C(-4,0)为焦点,即2c=8,c=4;实轴长为4,即a=2的双曲线的右支上,
∴b2=c2-a2=16-4=12.
又A、B、C构成三角形,故点C与A,B不共线,
∴顶点A的轨迹方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$(x>2).
故答案为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$(x>2).
点评 本题考查正弦定理,考查双曲线的概念与标准方程,考查理解与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
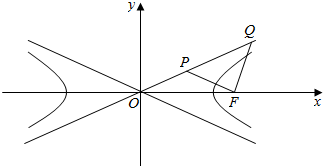
5.如图,已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,P、Q在渐近线上,PQ的中垂线过点F,O是坐标原点,若∠PFQ=Rt∠,OQ=3OP,则双曲线的离心率等于( )

| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
15.已知$\overrightarrow{a}$=(1-t,2t-1,0),$\overrightarrow{b}$=(2,t,2t),则|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
2.命题“?x∈R,ex>x2”的否定是( )
| A. | 不存在x∈R,使ex>x2 | B. | ?x0∈R,使ex0<x02 | ||
| C. | ?x0∈R,使ex0≤x02 | D. | ?x∈R,使ex≤x2 |
19.若实数x、y满足约束条$\left\{\begin{array}{l}{3x-y-3≤0}\\{x-2y+4≥0}\\{2x+y-2≤0}\end{array}\right.$,则z=x+y的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
16.已知$sinθ=\frac{4}{5}$,$cosθ=-\frac{3}{5}$,则2θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
17.f(x)=-$\frac{1}{2}$x2+bln(x+2)在(-1,+∞)上单调递减,则b的取值范围是( )
| A. | (-∞,-1) | B. | (-1,+∞) | C. | [-1,+∞) | D. | (-∞,-1] |