题目内容
1.已知函数f(x)=x+sinx(x∈R),且f(y2-8x+1)+f(x-6y+10)≤0,则当y≥3时,函数F(x,y)=x2+y2的最小值与最大值的和为62.分析 运用奇偶性的定义和求导,判断单调性,可得f(x)在R上为增函数.且为奇函数.由条件可得f(y2-8x+1)≤-f(x-6y+10)=f(-x+6y-10),则有y2-8x+11≤-x2+6y-10,运用配方可得(x-4)2+(y-3)2≤4,由圆的知识,及F(x,y)=x2+y2的几何意义是(x,y)与原点的距离的平方,即可得到最值之和.
解答 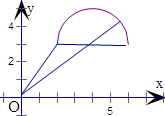 解:易知f(x)=x+sinx(x∈R),
解:易知f(x)=x+sinx(x∈R),
f(-x)=-x+sin(-x)=-(x+sinx)=-f(x),
则f(x)是奇函数,又f′(x)=1+cosx≥0,
则f(x)在R上为增函数.
所以f(y2-8x+1)+f(x2-6y+10)≤0,
即为f(y2-8x+1)≤-f(x2-6y+10)=f(-x2+6y-10),
则有y2-8x+11≤-x2+6y-10
即x2+y2-8x-6y+21≤0,即为(x-4)2+(y-3)2≤4,
又y≥3,则(x,y)对应可行域是以(4,3)为圆心,2为半径的上半圆面,
函数F(x,y)=x2+y2的几何意义是(x,y)与原点的距离的平方.
连接点(2,3)和(0,0)的距离为$\sqrt{13}$,连接原点和圆心(4,3)延长交半圆于P,
则PO的距离为$\sqrt{{4}^{2}+{3}^{2}}$+2=7,
即有F(x,y)min=13,F(x,y)max=49,其和为62.
故答案为:62.
点评 本题考查函数的奇偶性和单调性的运用,同时考查圆的方程,两点的距离公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
11.$n=\int\begin{array}{l}2\\ 0\end{array}(3{x^2}-1)dx$,则二项式${(x-\frac{1}{x^2})^n}$展开式中的常数项为( )
| A. | 2 | B. | 6 | C. | 12 | D. | 15 |
9.命题:在三角形中,顶点与对边中点连线所得三线段交于一点,且分线段长度比为2:1,类比可得在四面体中,顶点与所对面的( )连线所得四线段交于一点,且分线段比为( )
| A. | 重心 3:1 | B. | 垂心 3:1 | C. | 内心 2:1 | D. | 外心 2:1 |
6.已知数列{an}中,a1=1,an+1=-$\frac{1}{{{a_n}+1}}$,则a2015等于( )
| A. | 1 | B. | -1 | C. | $-\frac{1}{2}$ | D. | -2 |