题目内容
3.已知f(x)=$\left\{{\begin{array}{l}{\frac{x-1}{x-2},(x≤0)}\\{{{log}_2}x,(x>0)}\end{array}}$,则关于x的不等式f(x)>$\frac{1}{2}$的解集为{x|x<0或x$>\sqrt{2}$}.分析 当x>0时,原不等式可化为${log}_{2}x>\frac{1}{2}$,当x≤0时,原不等式可化为$\frac{x-1}{x-2}>\frac{1}{2}$,解不等式即可求解
解答 解:当x>0时,原不等式可化为${log}_{2}x>\frac{1}{2}$,
解不等式可得,x$>\sqrt{2}$
此时x$>\sqrt{2}$
当x≤0时,原不等式可化为$\frac{x-1}{x-2}>\frac{1}{2}$,解可得,x<0
此时x<0
综上可得,原不等式的解集为{x|x<0或x$>\sqrt{2}$}
故答案为:{x|x<0或x$>\sqrt{2}$}
点评 本题主要考查了分式不等式及对数不等式的求解,解题中要注意分类 讨论的应用.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
13.已知集合A={y|y=x2},B={x|y=lg(1-x)},则A∩B=( )
| A. | [0,1] | B. | [0,1) | C. | (-∞,1) | D. | (-∞,1] |
18.已知x∈(-$\frac{π}{2}$,0)且cosx=$\frac{\sqrt{3}}{2}$,则tan2x=( )
| A. | $\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
8.执行如图所示的算法,则输出的结果是( )
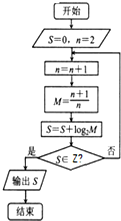

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20. 如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
 如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )
如图,梯形ABCD中,AD∥BC,DC⊥BC,AD=2,BC=6,若以AB为直径的⊙O与CD相切于点E,则DE等于( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | 8 |
 如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.
如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.