题目内容
14.已知等差数列{an}和公比大于1的等比数列{bn}满足a1=b1=1,a2=b2,a5=b3.(1)求数列{an},{bn}的通项公式;
(2)若数列{anbn}的前n项和为Sn,且对任意n∈N*均有λ[an+1bn+1-2(Sn-1)]>n2+n成立,求实数λ的取值范围.
分析 (1)利用等差数列、等比数列的通项公式,列出方程组,即可求出向量的通项;
(2)利用错位相减法,即可求数列{anbn}的前n项和为Sn,通过计算、变形可得问题即求函数y=f(x)=$\frac{{x}^{2}+x}{{3}^{x+1}}$当x取正整数时的最大值,计算即可.
解答 解:(1)设数列{an}的公差为d,数列{bn}的公比q>1,
∵a1=b1=1,
∴a2=1+d,b2=q,a5=1+4d,b3=q2,
∴(1+d)2=1•(1+4d),且1+d=q,
解得d=2,∴q=3,
∴an=1+2(n-1)=2n-1,
bn=1•3n-1=3n-1;
(2)由(1)知,Sn=1×1+3×3+5×32+…+(2n-1)•3n-1 ①
∴3Sn=1×3+3×32+…+(2n-3)•3n-1+(2n-1)•3n ②
①-②:-2Sn=1+2×(3+32+…+3n-1)-(2n-1)•3n ,
∴Sn=(n-1)•3n+1,
∴Sn-1=(n-1)•3n.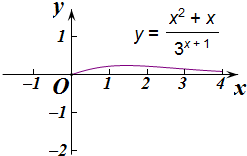
又∵an+1bn+1=(2n+1)•3n,
∴an+1bn+1-2(Sn-1)=3n+1,
∴λ[an+1bn+1-2(Sn-1)]>n2+n等价于λ>$\frac{{n}^{2}+n}{{3}^{n+1}}$,
记y=f(x)=$\frac{{x}^{2}+x}{{3}^{x+1}}$,当x>0时其图象如图,
∵f(1)=f(2)=$\frac{2}{9}$,
∴λ≥$\frac{2}{9}$.
点评 本题考查等差数列与等比数列的基本关系式,考查错位相减法的应用,考查计算能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
4.在不等式组$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥0}\\{y≤a}\end{array}\right.$确定的平面区域中,若z=x+2y的最大值为9,则a的值为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
5.已知集合M={x|x2-4x>0},N={x|m<x<8},若M∩N={x|6<x<n},则m+n=( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
2.复数$\frac{(1+i)^{2}}{1-i}$=( )
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
6. 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
 如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
 已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.
已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.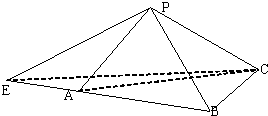 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.
如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.