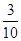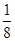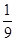题目内容
f(x)=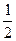 x2+
x2+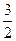 x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令bn=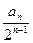 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn
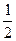 x2+
x2+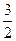 x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令bn=
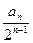 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn解:(Ⅰ)∵点(n,Sn)在f(x)的图象上,
∴Sn=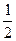 n2+
n2+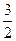 n.
n.
当n≥2时,an=Sn-Sn-1=n+1;当n=1时,a1=S1=2,满足上式,∴an=n+1(n∈N*).
(Ⅱ)bn=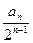 =
= ,
,
Tn=b1+b2+…+bn=2+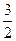 +…+
+…+ ,①
,①
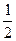 Tn=
Tn= +
+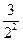 +…+
+…+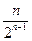 +
+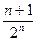 ,②
,②
由①-②,得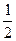 Tn=2+
Tn=2+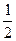 +
+ +…+
+…+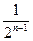 -
-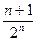 =(1+
=(1+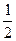 +
+ +…+
+…+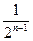 )+(1-
)+(1-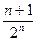 )=
)=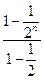 +1-
+1-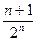 =2(1-
=2(1-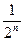 )+1-
)+1-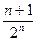 ,
,
∴Tn=6- .
.
∴Sn=
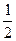 n2+
n2+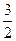 n.
n.当n≥2时,an=Sn-Sn-1=n+1;当n=1时,a1=S1=2,满足上式,∴an=n+1(n∈N*).
(Ⅱ)bn=
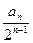 =
= ,
,Tn=b1+b2+…+bn=2+
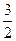 +…+
+…+ ,①
,①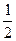 Tn=
Tn= +
+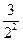 +…+
+…+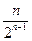 +
+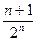 ,②
,②由①-②,得
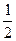 Tn=2+
Tn=2+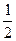 +
+ +…+
+…+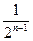 -
-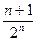 =(1+
=(1+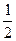 +
+ +…+
+…+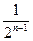 )+(1-
)+(1-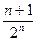 )=
)=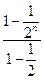 +1-
+1-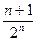 =2(1-
=2(1-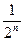 )+1-
)+1-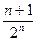 ,
,∴Tn=6-
 .
.略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
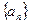 各项均为正数,
各项均为正数,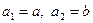 ,且对于正整数
,且对于正整数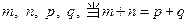 时,都有
时,都有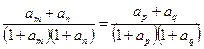 。
。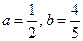 ,求
,求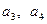 的值,并求数列
的值,并求数列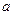 ,存在与
,存在与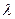 ,使得对于每个正整数
,使得对于每个正整数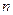 ,都有
,都有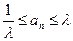 。
。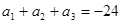 ,
,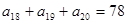 ,则此数列前20项和等于( )
,则此数列前20项和等于( )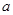 、
、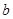 的等差中项是5,则
的等差中项是5,则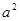 、
、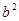 的等比中项的最大值为
的等比中项的最大值为 差数列{an}的公差d≠0,它的第1、5、17项顺次成等比数列,
差数列{an}的公差d≠0,它的第1、5、17项顺次成等比数列,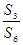 =
= ,则
,则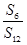 =( )
=( )