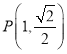题目内容
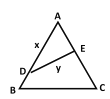
【题目】如图,公园有一块边长为![]() 的等边
的等边![]() 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(1)设![]() (
(![]() ),
),![]() ,求用
,求用![]() 表示
表示![]() 的函数关系式;
的函数关系式;
(2)如果![]() 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,![]() 的位置应在哪里?如果
的位置应在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长,![]() 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为
为![]() 中线或
中线或![]() 中线,理由见解析.
中线,理由见解析.
【解析】
试题分析:(1)在![]() 中,利用余弦定理有
中,利用余弦定理有![]() ,依题意
,依题意![]() ,即
,即![]() ,
,![]() ,由此求得
,由此求得![]() ;(2)如果
;(2)如果![]() 是水管,利用基本不等式可求得最小值为
是水管,利用基本不等式可求得最小值为![]() ,此时
,此时![]() ,即
,即![]() ,且
,且![]() 时,
时,![]() 最短.如果
最短.如果![]() 是参观线路,注意到
是参观线路,注意到![]() 在
在![]() 时值相等,根据对钩函数的性质可知最大值为
时值相等,根据对钩函数的性质可知最大值为![]()
试题解析:
(1)在![]() 中,
中,![]() ,即
,即![]() ,①
,①
又![]() ,即
,即![]() ,∴
,∴![]() ,②
,②
②代入①得:![]() (
(![]() ),∴
),∴![]() (
(![]() ).
).
(2)如果![]() 是水管,
是水管,![]() ,
,
当且仅当![]() ,即
,即![]() 时“
时“![]() ”成立,故
”成立,故![]() ,
,
即![]() ,且
,且![]() 时,
时,![]() 最短;
最短;
如果![]() 是参观线路,记
是参观线路,记![]() ,求导可知函数在
,求导可知函数在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
故![]() ,∴
,∴![]() ,
,
即![]() 为
为![]() 中线或
中线或![]() 中线时,
中线时,![]() 最长.
最长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目