题目内容
(1)直线l:y=x+b与抛物线C:x2=4y相切于点A,求实数b的值,及点A的坐标.
(2)在抛物线y=4x2上求一点,使这点到直线y=4x-5的距离最短.
(2)在抛物线y=4x2上求一点,使这点到直线y=4x-5的距离最短.
(1)由
得x2-4x-4b=0①.
因为直线l与抛物线C相切,所以△=16+16b=0,解得b=-1;
代入方程①即为x2-4x+4=0,解得x=2,所以y=1,
故点A(2,1).
(2)设点P(t,4t2),距离为d,
则d=
=
当t=
时,d取得最小值,此时P(
,1)为所求的点.
|
因为直线l与抛物线C相切,所以△=16+16b=0,解得b=-1;
代入方程①即为x2-4x+4=0,解得x=2,所以y=1,
故点A(2,1).
(2)设点P(t,4t2),距离为d,
则d=
| |4t-4t2-5| | ||
|
|4(t-
| ||
|
当t=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
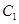 的方程为
的方程为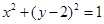 ,定直线
,定直线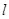 的方程为
的方程为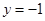 .动圆
.动圆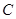 与圆
与圆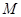 的方程;
的方程;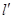 与轨迹
与轨迹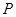 , 过点
, 过点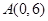 ,并交轨迹
,并交轨迹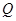 ,求直线
,求直线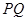 的方程及
的方程及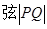 的长.
的长.