题目内容
10.对于函数f(x)、g(x),存在函数h(x),使得f(x)=g(x)•h(x),则称f(x)是g(x)的“h(x)关联函数”.(1)已知f(x)=sinx,g(x)=cosx,是否存在定义域为R的函数h(x),使得f(x)是g(x)的“h(x)关联函数”?若存在,写出h(x)的解析式;若不存在,请说明理由;
(2)已知函数f(x)、g(x)的定义域为[1,+∞),当x∈[n,n+1)时,f(x)=2n-1sin$\frac{x}{n}$-1,若存在函数h1(x)及h2(x),使得f(x)是g(x)的“h1(x)关联函数”,且g(x)是f(x)的“h2(x)关联函数”,求方程g(x)=0的解.
分析 (1)假设存在定义域为R的函数h(x),使得f(x)是g(x)的“h(x)关联函数”.再由同角的三角函数的关系式,即可判断;
(2)由题意可得f(x)=g(x)h1(x),g(x)=f(x)h2(x),相乘可得,h1(x)h2(x)=1,即有g(x)=0,即为f(x)=0,解三角方程,即可得到所求的解.
解答 解:(1)假设存在定义域为R的函数h(x),
使得f(x)是g(x)的“h(x)关联函数”.
即有sinx=cosx•h(x),解得h(x)=tanx,
由tanx的定义域为{x|x≠kπ+$\frac{π}{2}$,k∈Z},
故不存在定义域为R的函数h(x);
(2)由题意可得f(x)=g(x)h1(x),g(x)=f(x)h2(x),
相乘可得,h1(x)h2(x)=1,
即有g(x)=0,即为f(x)=0,
即2n-1sin$\frac{x}{n}$-1=0,即sin$\frac{x}{n}$=$\frac{1}{{2}^{n-1}}$,
解得$\frac{x}{n}$=2kπ+arcsin$\frac{1}{{2}^{n-1}}$或2kπ+π-arcsin$\frac{1}{{2}^{n-1}}$(k≥0且k∈Z),
即为x=n(2kπ+arcsin$\frac{1}{{2}^{n-1}}$)或n(2kπ+π-arcsin$\frac{1}{{2}^{n-1}}$)(k≥0且k∈Z).
点评 本题考查新定义的理解和运用,考查三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
相关题目
15.已知抛物线y=$\frac{{x}^{2}}{4}$与直线y=$\frac{3}{4}$x+1交于点P,Q,则如图所示阴影部分的面积为( )
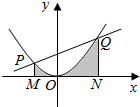

| A. | $\frac{65}{12}$ | B. | $\frac{85}{16}$ | C. | $\frac{143}{24}$ | D. | $\frac{95}{6}$ |
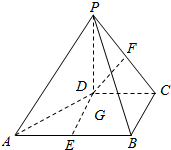 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.