��Ŀ����
17����֪����$\overrightarrow{m}$=��$\sqrt{3}$cos��x��cos��x����$\overrightarrow{n}$=��sin��x��-cos��x�����أ�0��������f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$����С������Ϊ$\frac{��}{2}$����1������f��x����
��2����ص�ֵ��
��3����mΪ��ֵʱ��ֱ��y=m�뺯��y=f��x����x��[0��$\frac{��}{4}$]��ͼ��ֻ��һ�����㣮
���� ��1�����������������㣬Ȼ����ݶ����ǵ������ҹ�ʽ�����Dz�����ҹ�ʽ���ɵó�f��x��=$sin��2��x-\frac{��}{6}��-\frac{1}{2}$��
��2������f��x������С������Ϊ$\frac{��}{2}$���У�$\frac{2��}{2��}=\frac{��}{2}$���Ӷ�����æ�=4��
��3�����������֪������m+$\frac{1}{2}$=$sin��4x-\frac{��}{6}��$ֻ��һ���⣬�ɻ�Ԫ����4x-$\frac{��}{6}$=t���Ӷ��ó�ֱ��y=m+$\frac{1}{2}$��y=sint����t$��[-\frac{��}{6}��\frac{5��}{6}]$��ֻ��һ�����㣬�����������Һ�����$[-\frac{��}{6}��\frac{5��}{6}]$�ϵ�ͼ�ɵó�m��ȡֵ��
��� �⣺��1��$\overrightarrow{m}•\overrightarrow{n}=\sqrt{3}sin��xcos��x-co{s}^{2}��x$=$\frac{\sqrt{3}}{2}sin2��x-\frac{1+cos2��x}{2}$=$sin��2��x-\frac{��}{6}��-\frac{1}{2}$��
��$f��x��=sin��2��x-\frac{��}{6}��-\frac{1}{2}$��
��2����f��x������С������Ϊ$\frac{��}{2}$��
��$\frac{2��}{2��}=\frac{��}{2}$��
���=2��
��3��$f��x��=sin��4x-\frac{��}{6}��-\frac{1}{2}$��
�������⣬����$m=sin��4x-\frac{��}{6}��-\frac{1}{2}$ֻ��һ���⣻
������$m+\frac{1}{2}=sin��4x-\frac{��}{6}��$ֻ��һ���⣬��4x-$\frac{��}{6}$=t��$t��[-\frac{��}{6}��\frac{5��}{6}]$��
��ֱ��y=$m+\frac{1}{2}$��y=sint��t$��[-\frac{��}{6}��\frac{5��}{6}]$ֻ��һ�����㣬��ͼ��ʾ��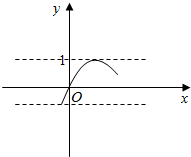
����ͼ��y=1��y=-$\frac{1}{2}$����y=sint��[$-\frac{��}{6}��\frac{5��}{6}$]��ֻ��һ�����㣻
��$m=\frac{1}{2}$����m=-1ʱ��ֱ��y=m�ͺ���y=f��x����x$��[0��\frac{��}{4}]$��ͼ��ֻ��һ�����㣮
���� �������������������㣬�����ǵ������ҹ�ʽ�����Dz�����ҹ�ʽ���Լ����Ǻ������ڵĸ������ֱ�ߺ����߽���Ͷ�Ӧ��ֱ�߷��̺����߷����γɷ������Ĺ�ϵ�����ν�Ͻ���ķ�������Ϥ���Һ���ͼ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | a��0 | B�� | a��0 | C�� | a��0 | D�� | aΪ����ʵ�� |
| A�� | ����ƽ��$\frac{��}{3}$����λ | B�� | ����ƽ��$\frac{��}{6}$����λ | ||
| C�� | ����ƽ��$\frac{��}{3}$����λ | D�� | ����ƽ��$\frac{��}{6}$����λ |