题目内容

11．已知a、b∈R，a+b=1，用分析法证明：（a+2）2+（b+2）2≥$\frac{25}{2}$．

分析 寻找使不等式：（a+2）2+（b+2）2≥$\frac{25}{2}$成立的充分条件，直到使不等式成立的充分条件已经显然具备为止．

解答 证明：要证：（a+2）2+（b+2）2≥$\frac{25}{2}$，
只要证：a2+b2+4（a+b）+8≥$\frac{25}{2}$，
∵a+b=1，
∴只要证a2+b2≥$\frac{1}{2}$，
∴即证a2+（1-a）2≥$\frac{1}{2}$
只要证（a-$\frac{1}{2}$）2≥0，
显然成立，故原不等式成立．

点评 本题主要考查基本不等式的应用，用分析法证明不等式，利用用分析法证明不等式的关键是寻找使不等式成立的充分条件，直到使不等式成立的充分条件已经显然具备为止，属于中档题．

练习册系列答案
相关题目
10．已知f（x）=|x2-4x|，g（x）=ln|x-2|，则方程f（x）=g（x）所有实根之和为（　　）
A．4B．6C．8D．10
2．空间四边形ABCD中，对角线AC，BD与各边长均为1，O为△BCD的重心，M是AC的中点，E是AO的中点，求异面直线OM与BE所成的角为$\frac{π}{4}$．
19．已知向量$\overrightarrow{a}$=（cos$\frac{3x}{2}$，sin$\frac{3x}{2}$），$\overrightarrow{b}$=（cos$\frac{x}{2}$，-sin$\frac{x}{2}$），x∈[0，$\frac{π}{2}$]
（1）求函数$f（x）=\overrightarrow a•\overrightarrow b-2|\overrightarrow a+\overrightarrow b|$的值域；
（2）设g（x）=$\overrightarrow{a}$•$\overrightarrow{b}$+t|$\overrightarrow{a}$+$\overrightarrow{b}$|，若关于x的方程g（x）+2=0有两个不同的实数解，求实数t的取值范围．
6．若y=f（x）为R上的减函数，z=af（x）为R上的增函数，则实数a的值为（　　）
A．a＜0B．a＞0C．a≤0D．a为任意实数
16．实数a，b∈R，i是虚数单位，若a+2i与2-bi互为共轭复数，则a+b=4．
3．已知数列{an}是递增的等比数列，且a3+a6=9，a2a7=8．
（1）求数列{an}的通项公式；
（2）设Sn为数列{an}的前n项和，${b_n}=\frac{{{a_{n+1}}}}{{{S_n}{S_{n+1}}}}$，求数列{bn}的前n项和Tn；
（3）对于（2）中的Tn，若Tn＜m-2014对一切n∈N*成立，求最小正整数m．
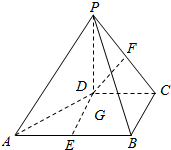20．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=CB=1，BA=2，AB∥DC，∠BCD=90°，点E、F、G分别是线段AB、PC、DE的中点．
（Ⅰ）求证：FG∥平面PAB；
（Ⅱ）求证：DF⊥平面PBC．
1．在△ABC中，a，b，c分别是角A、B、C的对边，且$\sqrt{3}$acosB+bsinA=0．
（I）求角B的大小；
（Ⅱ）若△ABC的面积S=$\sqrt{3}$，a=1，求b．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网