题目内容
2.已知圆O的方程为x2+y2=8.(Ⅰ)若直线l:3x+4y-8=0,试判断直线l与圆O的位置关系;
(Ⅱ)点A(2,y0)在圆O上,且y0>0,在圆O上任取不重合于A的两点M,N,若直线AM和AN的斜率存在且互为相反数,试问:直线MN的斜率是否为定值?若是,求出该定值;若不是,说明理由.
分析 (Ⅰ)求出圆心到直线l:3x+4y-8=0的距离与半径比较,即可判断直线l与圆O的位置关系;
(Ⅱ)求出M,N的坐标,即可求出直线MN的斜率.
解答 解:(Ⅰ)圆O的圆心为(0,0),半径为2$\sqrt{2}$,
圆心到直线l:3x+4y-8=0的距离d=$\frac{8}{5}$<2$\sqrt{2}$,
∴直线l与圆O相交;
(Ⅱ)由点A(2,y0)在圆O上,且y0>0,可得y0=2.
设直线AM的斜率为k,则直线AM的方程为y=kx+2-2k,
代入圆O,可得(1+k2)x2+4k(1-k)x+4(k2-2k-1)=0,
∵2是方程的一个根,
∴2xM=$\frac{4({k}^{2}-2k-1)}{{k}^{2}+1}$,∴xM=$\frac{2({k}^{2}-2k-1)}{{k}^{2}+1}$.
由题意,kAN=-k,∴xN=$\frac{2({k}^{2}+2k-1)}{{k}^{2}+1}$,
∴kMN=$\frac{k({x}_{M}+{x}_{N}-4)}{{x}_{M}-{x}_{N}}$=k•$\frac{\frac{-8}{1+{k}^{2}}}{\frac{-8k}{1+{k}^{2}}}$=1,
∴直线MN的斜率是定值1.
点评 本题考查直线与圆的位置关系,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.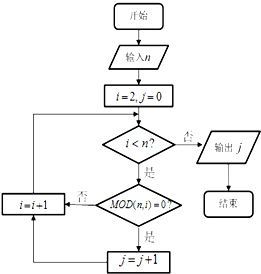 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )
 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入的值为36时,则输出的结果为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
17.已知x>0,y>0,若$\frac{2y}{x}$+$\frac{8x}{y}$>a2+2a恒成立,则实数a的取值范围是( )
| A. | a≥4或a≤-2 | B. | a≥2或a≤-4 | C. | -2<a<4 | D. | -4<a<2 |
11.已知A,B是抛物线y2=4x上异于顶点O的两个点,直线OA与直线OB的斜率之积为定值-4,F为抛物线的焦点,△AOF,△BOF的面积分别为S1,S2,则S12+S22的最小值为( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
15.甲、乙两人抢答竞赛题,甲答对的概率为$\frac{1}{5}$,乙答对的概率为$\frac{1}{4}$,则两人恰有一人答对的概率为( )
| A. | $\frac{7}{20}$ | B. | $\frac{12}{20}$ | C. | $\frac{1}{20}$ | D. | $\frac{2}{20}$ |
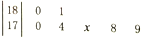 一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图所示,已知记录的平均身高为177cm,有1名选手的身高记录不清楚,其末位数记为x,那么x的值为( )
一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图所示,已知记录的平均身高为177cm,有1名选手的身高记录不清楚,其末位数记为x,那么x的值为( )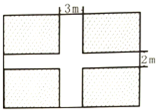 某校计划新建一个占地面积为600m2的停放自行车的矩形场地,在矩形场地中间保留宽分别为2m和3m的十字型通道,如图所示,当矩形用地的边长各为多少时,自行车停放地(阴影部分)的占地面积最大?最大面积是多少?
某校计划新建一个占地面积为600m2的停放自行车的矩形场地,在矩形场地中间保留宽分别为2m和3m的十字型通道,如图所示,当矩形用地的边长各为多少时,自行车停放地(阴影部分)的占地面积最大?最大面积是多少?