题目内容
7.化简求值:(1)tan70°cos10°($\sqrt{3}$tan20°-1)
(2)已知cos($\frac{π}{4}$+x)=$\frac{3}{5}$,$\frac{17π}{12}$<x<$\frac{7π}{4}$,求$\frac{sin2x+2si{n}^{2}x}{1-tanx}$的值.
分析 (1)由条件利用三角恒等变换化简要求的式子,可得结果.
(2)由条件利用同角三角函数的基本关系求得 tan(x+$\frac{π}{4}$)的值,再化简要求的式子为-[2${cos}^{2}(x+\frac{π}{4})$-1]•tan(x+$\frac{π}{4}$),从而得到结果.
解答 解:(1)tan70°cos10°($\sqrt{3}$tan20°-1)=$\frac{sin70°}{cos70°}$•cos10°•$\frac{\sqrt{3}sin20°-cos20°}{cos20°}$=$\frac{cos20°}{sin20°}$•cos10°•$\frac{2sin(20°-30°)}{cos20°}$
=cos10°$\frac{-2sin10°}{sin20°}$=-1.
(2)∵cos($\frac{π}{4}$+x)=$\frac{3}{5}$,$\frac{17π}{12}$<x<$\frac{7π}{4}$,∴x+$\frac{π}{4}$∈($\frac{5π}{3}$,2π),∴sin(x+$\frac{π}{4}$)=-$\sqrt{{1-cos}^{2}(x+\frac{π}{4})}$=-$\frac{4}{5}$,∴tan(x+$\frac{π}{4}$)=-$\frac{4}{3}$.
∴$\frac{sin2x+2si{n}^{2}x}{1-tanx}$=$\frac{2sinxcosx(cosx+sinx)}{cosx-sinx}$=sin2x•$\frac{1+tanx}{1-tanx}$=-cos(2x+$\frac{π}{2}$)=-[2${cos}^{2}(x+\frac{π}{4})$-1]•tan(x+$\frac{π}{4}$)
=-[2×$\frac{9}{25}$-1]•(-$\frac{4}{3}$)=-$\frac{28}{75}$.
点评 本题主要考查三角恒等变换及化简求值,属于中档题.

| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $\frac{1}{a^2}>\frac{1}{b^2}$ | C. | a2>b2 | D. | 2a>2b |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | -e | B. | e | C. | -e-1 | D. | e-1 |
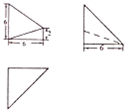 已知某空间几何体的三视图如图所示,则该几何体的体积是( )
已知某空间几何体的三视图如图所示,则该几何体的体积是( )| A. | 16 | B. | 32 | C. | 36 | D. | 48 |
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |