题目内容
11.已知A,B是抛物线y2=4x上异于顶点O的两个点,直线OA与直线OB的斜率之积为定值-4,F为抛物线的焦点,△AOF,△BOF的面积分别为S1,S2,则S12+S22的最小值为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 通过设A(x1,y1)、B(x2,y2),利用$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=-4化简得y1y2=-4,通过三角形面积公式及基本不等式计算即得结论.
解答 解:设A(x1,y1),B(x2,y2),
∵直线OA与直线OB的斜率之积为定值-4,
∴$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=-4,即$\frac{{y}_{1}{y}_{2}}{\frac{{{y}_{1}}^{2}}{4}•\frac{{{y}_{2}}^{2}}{4}}$=-4,
化简得:y1y2=-4,
∵△AOF、△BOF的面积为S1、S2,
∴S12+S22=$\frac{1}{4}$(y12+y22)≥$\frac{1}{4}$•2|y1y2|=2(当且仅当|y1|=|y2|时取等号),
故选:D.
点评 本题考查抛物线的简单性质,注意解题方法的积累,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
1.直线y=a与y=tanx的图象的相邻两个交点的距离是( )
| A. | $\frac{π}{2}$ | B. | π | ||
| C. | 2π | D. | 与a的值的大小有关 |
19.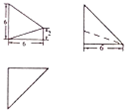 已知某空间几何体的三视图如图所示,则该几何体的体积是( )
已知某空间几何体的三视图如图所示,则该几何体的体积是( )
 已知某空间几何体的三视图如图所示,则该几何体的体积是( )
已知某空间几何体的三视图如图所示,则该几何体的体积是( )| A. | 16 | B. | 32 | C. | 36 | D. | 48 |
6.用反证法证明命题:“若a1+a2+a3+a4>100,则a1,a2,a3,a4中至少有一个数大于25.”时,假设的内容应为( )
| A. | a1,a2,a3,a4都大于25 | B. | a1,a2,a3,a4都小于25 | ||
| C. | a1,a2,a3,a4都不大于25 | D. | a1,a2,a3,a4都不小于25 |
16.抛物线y2=2px(p>0)的焦点为F,点A,B在此抛物线上,且∠AFB=90°,弦AB的中点M在该抛物线准线上的射影为M′,则$\frac{|MM′|}{|AB|}$的最大值为( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
3.已知集合A={x|(x-2)(x+3)<0},x∈R},B={x|1≤x≤3,x∈R },则A∩B=( )
| A. | [1,2) | B. | [1,2] | C. | (2,3] | D. | [2.3] |
4.不等式(x2-1)(x+1)≤0的解集为( )
| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-∞,1) | D. | (-∞,1] |