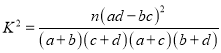题目内容
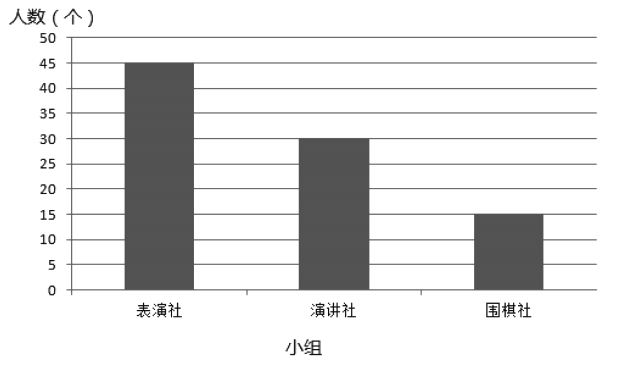
【题目】我市正在创建全国文明城市，某高中为了解学生的创文知晓率，按分层抽样的方法从“表演社”、“演讲社”、“围棋社”三个活动小组中随机抽取了6人进行问卷调查，各活动小组人数统计如下图：
（1）从参加问卷调查的6名学生中随机抽取2名，求这2名学生来自同一小组的概率；
（2）从参加问卷调查的6名学生中随机抽取3名，用
表示抽得“表演社”小组的学生人数，求的分布列及数学期望.
【答案】（1）
（2）详见解析
【解析】
（1）由题意按分层抽样的方法抽取6人，则三个小组分别抽取3人，2人，1人.利用古典概型计算公式得到这2名学生来自同一小组的概率；
（2）X的可能取值为0，1，2，3，分别求出相应的概率，由此能求出X的分布列和数学期望．
解：（1）由条件可知，表演社、演讲社、围棋社分别有45人、30人、15人，从中按分层抽样的方法抽取6人，则三个小组分别抽取3人，2人，1人.
从中抽取2名，则这2名学生来自同一小组的概率为
.
（2）
的所有可能取值为0,1,2,3，
，
，
，
，
所以的分布列为
.
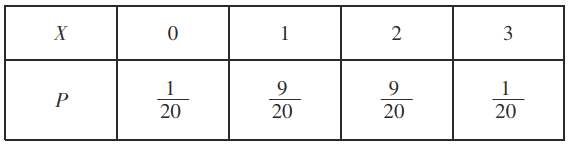
练习册系列答案
相关题目
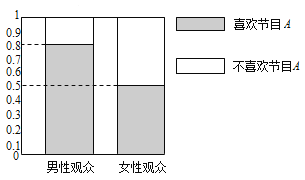
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
（1）请将上面的列联表补充完整;
（2）能否在犯错概率不超过
的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式: 
)
临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
