题目内容
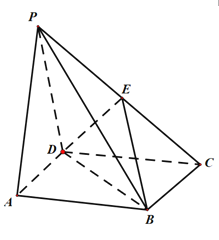
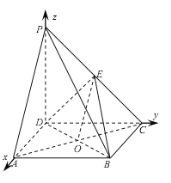
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 若直线
若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用线面平行的判定定理,即可证得
,利用线面平行的判定定理,即可证得![]() 平面
平面![]() ;
;
![]() 以
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,
,![]() ,分别求得平面
,分别求得平面![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() 和
和![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
由题意可知,![]() ,
,![]() ,
,
又![]() 在平面
在平面![]() 外,
外,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 以
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
由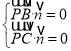 ,得
,得![]() ,取
,取![]() ,
,
又由直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
得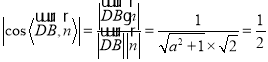 ,解得
,解得![]() ,
,
同理可得平面![]() 的法向量
的法向量![]() ,
,
由向量的夹角公式,可得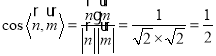 ,
,
又因为二面角![]() 为锐二面角,所以二面角
为锐二面角,所以二面角![]() 的大小为
的大小为![]() .
.

【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.