题目内容
(本题满分12分) 设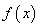 是定义在
是定义在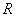 上的增函数,令
上的增函数,令
(1)求证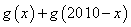 时定值;
时定值;
(2)判断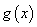 在
在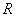 上的单调性,并证明;
上的单调性,并证明;
(3)若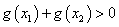 ,求证
,求证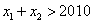 。
。
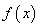 是定义在
是定义在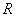 上的增函数,令
上的增函数,令
(1)求证
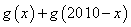 时定值;
时定值;(2)判断
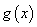 在
在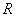 上的单调性,并证明;
上的单调性,并证明;(3)若
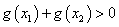 ,求证
,求证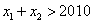 。
。(1)0(2)增函数(3)见解析
解:(1)∵
∴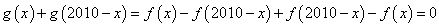 为定值
为定值
(2)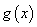 在
在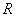 上的增函数 设
上的增函数 设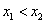 ,则
,则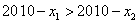
∵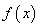 是
是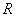 上的增函数∴
上的增函数∴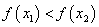 ,
,
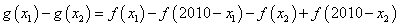
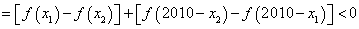
即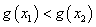 ,∴
,∴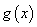 在
在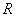 上的增函数
上的增函数
(3)假设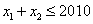 ,则
,则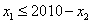
故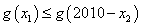
又
∴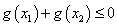 ,与已知
,与已知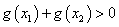 矛盾
矛盾
 ∴
∴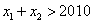

∴
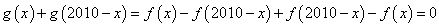 为定值
为定值 (2)
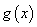 在
在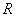 上的增函数 设
上的增函数 设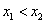 ,则
,则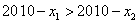
∵
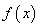 是
是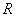 上的增函数∴
上的增函数∴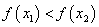 ,
,
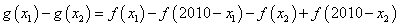
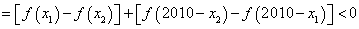
即
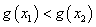 ,∴
,∴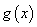 在
在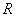 上的增函数
上的增函数(3)假设
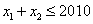 ,则
,则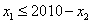
故
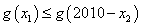
又

∴
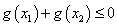 ,与已知
,与已知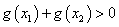 矛盾
矛盾  ∴
∴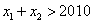

练习册系列答案
相关题目
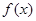 的最小值为1,且
的最小值为1,且 .
. 上不单调,求
上不单调,求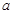 的取值范围.
的取值范围.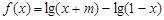 .
.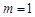 时,判断函数
时,判断函数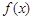 的奇偶性;
的奇偶性;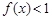 的解集为A,且
的解集为A,且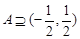 ,求实数
,求实数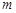 的取值范围.
的取值范围.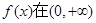 上是增函数,且
上是增函数,且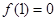 ,则不等式
,则不等式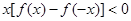 的解集为( )
的解集为( )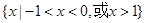

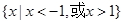
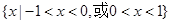
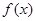 是R上的单调函数,且"x∈R,
是R上的单调函数,且"x∈R,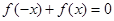 ,若
,若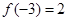
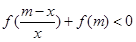 ,其中m∈R且m > 0
,其中m∈R且m > 0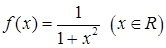 的值域是( )
的值域是( )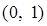
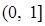
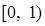
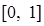
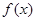 的定义域为
的定义域为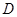 ,若
,若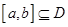 ,使
,使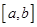 上的值域为
上的值域为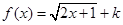 为闭函数,那么
为闭函数,那么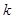 的取值范围是_______。
的取值范围是_______。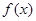 的定义域为
的定义域为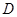 ,若存在非零常数
,若存在非零常数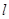 使得对于任意
使得对于任意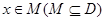 有
有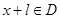 且
且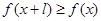 ,则称
,则称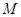 上的
上的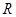 的奇函数
的奇函数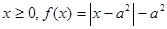 ,若
,若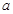 的取值范围为________.
的取值范围为________.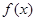 是定义在
是定义在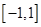 上的增函数,且
上的增函数,且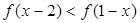 ,则
,则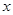 的取值范围为
的取值范围为