题目内容
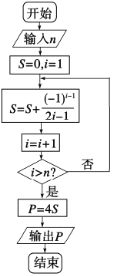
【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入
,则输出的结果是( )
A.
B.
C.
D.
【答案】B
【解析】
执行给定的程序框图，输入
，逐次循环，找到计算的规律，即可求解.
由题意，执行给定的程序框图，输入，可得：
第1次循环：
；
第2次循环：
；
第3次循环：
；
第10次循环：
，
此时满足判定条件，输出结果
，
故选：B.
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案【题目】某市垃圾处理厂的垃圾年处理量（单位：千万吨）与资金投入量x（单位：千万元）有如下统计数据：
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
资金投入量x（千万元） | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾处理量y（千万吨） | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
（1）若从统计的5年中任取2年，求这2年的垃圾处理量至少有一年不低于8.0（千万吨）的概率；
（2）由表中数据求得线性回归方程为
，该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨，现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元，请你预测2017年能否完成垃圾处理任务，若不能，缺口约为多少千万吨？
【题目】自2017年起，部分省、市陆续实施了新高考，某省采用了“
”的选科模式，即：考试除必考的语、数、外三科外，再从物理、化学、生物、历史、地理、政治六个学科中，任意选取三科参加高考，为了调查新高考中考生的选科情况，某地区调查小组进行了一次调查，研究考生选择化学与选择物理是否有关.已知在调查数据中，选物理的考生与不选物理的考生人数相同，其中选物理且选化学的人数占选物理人数的
，在不选物理的考生中，选化学与不选化学的人数比为
.
（1）若在此次调查中，选物理未选化学的考生有100人，试完成下面的列联表：
选化学 | 不选化学 | 合计（人数） | |
选物理 | |||
不选物理 | |||
合计（人数） |
（2）根据第（1）问的数据，能否有99%把握认为选择化学与选择物理有关？
（3）若研究得到在犯错误概率不超过0.01的前提下，认为选化学与选物理有关，则选物理又选化学的人数至少有多少？（单位：千人；精确到0.001）
附：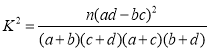
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
