题目内容
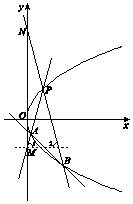
【题目】在平面直角坐标系xOy中，抛物线C的顶点是原点，以x轴为对称轴，且经过点P（1，2）． （Ⅰ）求抛物线C的方程；
（Ⅱ）设点A，B在抛物线C上，直线PA，PB分别与y轴交于点M，N，|PM|=|PN|．求直线AB的斜率．
【答案】解：（Ⅰ）依题意，设抛物线C的方程为y2=ax（a≠0）．
由抛物线C经过点P（1，2），
得a=4，
所以抛物线C的方程为y2=4x．
（Ⅱ）因为|PM|=|PN|，
所以∠PMN=∠PNM，
所以∠1=∠2，
所以直线PA与PB的倾斜角互补，
所以kPA+kPB=0．
依题意，直线AP的斜率存在，设直线AP的方程为：y﹣2=k（x﹣1）（k≠0），
将其代入抛物线C的方程，整理得k2x2﹣2（k2﹣2k+2）x+k2﹣4k+4=0．
设A（x1，y1），则x1= 
，y1= 
﹣2，
所以A（ ， ﹣2）．
以﹣k替换点A坐标中的k，得B（ 
，﹣ ﹣2．
所以 kAB= 
=﹣1，
所以直线AB的斜率为﹣1．
【解析】（Ⅰ）根据抛物线C经过点P（1，2），求抛物线C的方程；（Ⅱ）由题意，直线PA与PB的倾斜角互补，所以kPA+kPB=0，求出A，B的坐标，即可得出结论．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
