题目内容
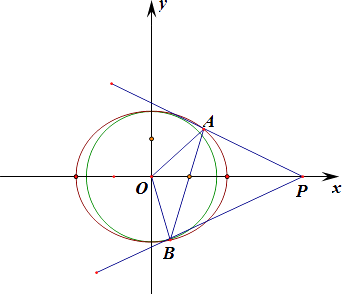
【题目】已知椭圆C: ![]() ,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
(Ⅱ)求证:以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
【答案】解:(Ⅰ)由题意可知:椭圆的焦点在x轴上,a=2,b= ![]() ,c=1,
,c=1,
则椭圆的离心率公式e= ![]() =
= ![]() ,
,
∴椭圆C的离心率 ![]() ;
;
(Ⅱ)证明:由c=1,则焦点F(1,0),当直线l的斜率不存在时,直线l的方程x=1,
A,B两点关于x轴对称,则P(4,0)在x轴上,
∴直线PA与直线PB关于x轴对称,
∴点O到直线PA的距离与到PB的距离相等,
∴以坐标原点O为圆心与PA相切的圆,必与直线PB相切,
当直线l的斜率存在时,设直线l:y=k(x﹣1),A(x1,y1),B(x2,y2),
由 ![]() ,整理得:(3+4k2)x2﹣8k2x+4k2﹣12=0,
,整理得:(3+4k2)x2﹣8k2x+4k2﹣12=0,
由韦达定理可知:x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
由kPA= ![]() =
= ![]() ,kPB=
,kPB= ![]() =
= ![]() ,
,
则kPA+kPB= ![]() +
+ ![]() =
= ![]() =
= 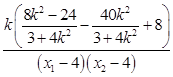 =0,
=0,
∴∠APO=∠BPO,则点O到直线PA和直线PB的距离相等,
∴以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
【解析】(Ⅰ)由椭圆方程,求得a和c的值,即可求得椭圆的离心率;(2)分类讨论,当直线斜率存在时,设直线方程,利用韦达定理及直线的斜率公式可知kPA+kPB=0,即可证明以坐标原点O为圆心与PA相切的圆,必与直线PB相切.

练习册系列答案
相关题目