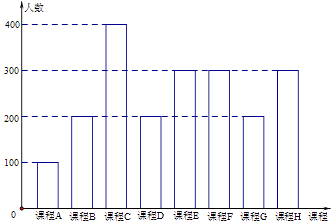
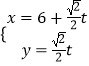题目内容
【题目】如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记∠AOP为x（x∈[0，π]），OP所经过的在正方形ABCD内的区域（阴影部分）的面积S=f（x），那么对于函数f（x）有以下三个结论，其中不正确的是（ ）
①f（ 
）= 
②函数f（x）在（ 
，π）上为减函数
③任意x∈[0， ]，都有f（x）+f（π﹣x）=4．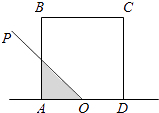
A.①
B.③
C.②
D.①②③
【答案】C
【解析】解：当0≤x≤arctan2时，f（x）= 
tanx；
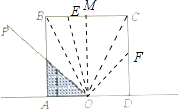
当arctan2＜x＜ 
，在△OBE中，f（x）=S矩形OABM﹣S△OME=2﹣ EMOM=2﹣ 
；
当x= 时，f（x）=2；
当 ＜x≤π﹣arctan2时，同理可得f（x）=2﹣ ．
当π﹣arctan2＜x≤π时，f（x）=4﹣ ×1×tan（π﹣x）=4+ tanx．于是可得：
①f（ 
）= tan = 
，正确；
②当 ＜x≤π﹣arctan2时，由f（x）=2﹣ ，为增函数．当π﹣arctan2＜x≤π时，f（x）=4+ tanx，为增函数，因此不正确．
③x∈[0， ]，由图形及其上面，利用对称性可得：f（x）+f（π﹣x）=4，因此正确；
所以答案是：C．
练习册系列答案
相关题目
