题目内容
数列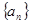 满足:
满足: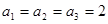 ,
,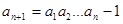 (
(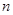 ≥3),记
≥3),记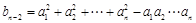
(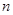 ≥3).
≥3).
(1)求证数列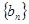 为等差数列,并求通项公式;
为等差数列,并求通项公式;
(2)设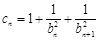 ,数列{
,数列{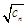 }的前n项和为
}的前n项和为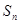 ,求证:
,求证: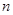 <
<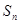 <
<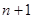 .
.
(1) (2)详见解析.
(2)详见解析.
解析试题分析:(1)本题实质由和项求通项:
当n≥3时,因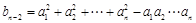 ①, 故
①, 故 ②,
②,
②-①,得 bn-1-bn-2= =
=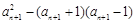 =1,为常数,所以,数列{bn}为等差数列因 b1=
=1,为常数,所以,数列{bn}为等差数列因 b1= =4,故
=4,故 (2)本题证明实质是求和,而求和关键在于对
(2)本题证明实质是求和,而求和关键在于对 开方:因
开方:因 
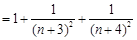
 ,
,
故 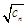
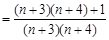
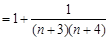
 .
.
所以 
 ,即 n<Sn
,即 n<Sn
又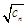 <
< ,于是
,于是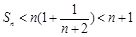 . 于是
. 于是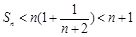
解 (1)方法一 当n≥3时,因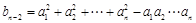 ①,
①,
故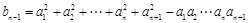 ② 2分
② 2分
②-①,得 bn-1-bn-2= =
=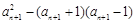 =1,为常数,所以,数列{bn}为等差数列 5分
=1,为常数,所以,数列{bn}为等差数列 5分
因 b1= =4,故
=4,故  8分
8分
方法二 当n≥3时,a1a2an="1+an+1," a1a2anan+1="1+an+2," 将上两式相除并变形,得  ------2分 于是,当n∈N*时,
------2分 于是,当n∈N*时, 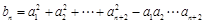

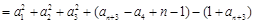
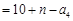 . 5分
. 5分
又a4=a1a2a3-1=7,故bn=n+3(n∈N*).
所以数列{bn}为等差数列,且bn=n+3 8分
(2) 因 
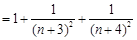
 , 10分
, 10分
故 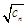
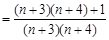
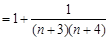
 . 12分
. 12分
所以 
 ,
,
即 n<Sn 。 14分
又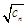 <
< ,于是
,于是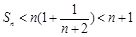 . 于是
. 于是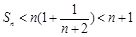 . 16分
. 16分
考点:等差数列定义,裂项求和

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上
的图象上 归纳数列
归纳数列 ),
), ,
, ,
, ;
; ,
, ,
, ,
, ;
; ,…..,
,….., ,
, 的值;
的值;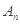 为数列
为数列 的前
的前 对一切
对一切 ,求
,求 的取值范围
的取值范围 中,
中, ,
,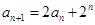 .
. .证明:数列
.证明:数列 是等差数列;(2)求数列
是等差数列;(2)求数列 项和
项和 .
.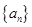 的前
的前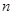 项和为
项和为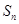 ,
,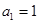 ,
,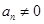 ,
,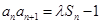 ,其中
,其中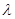 为常数,
为常数,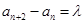 ;
;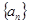 和
和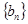 满足
满足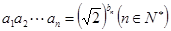 .若
.若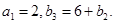
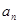 与
与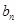 ;
;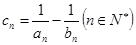 。记数列
。记数列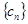 的前
的前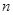 项和为
项和为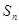 .
. ,使得对任意
,使得对任意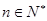 ,均有
,均有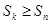 .
.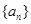 的公差为2,前
的公差为2,前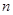 项和为
项和为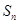 ,且
,且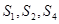 成等比数列.
成等比数列.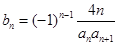 ,求数列
,求数列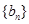 的前
的前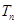 .
.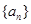 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, ,
,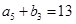 ,
,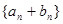 的前
的前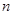 项和
项和 .
. }是等差数列,数列{
}是等差数列,数列{ }的前
}的前 项和
项和 满足
满足 ,
, ,
, 。
。 为数列{
为数列{