题目内容
已知数列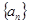 和
和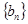 满足
满足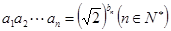 .若
.若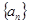 为等比数列,且
为等比数列,且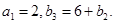
(1)求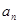 与
与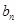 ;
;
(2)设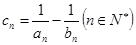 。记数列
。记数列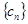 的前
的前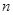 项和为
项和为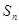 .
.
(i)求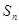 ;
;
(ii)求正整数 ,使得对任意
,使得对任意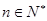 ,均有
,均有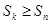 .
.
(1) ,
, ;(2)(i)
;(2)(i)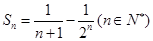 ;(ii)
;(ii)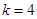 .
.
解析试题分析:(1)求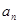 与
与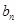 得通项公式,由已知
得通项公式,由已知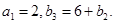 得
得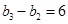 ,再由已知
,再由已知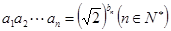 得,
得,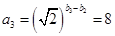 ,又因为数列
,又因为数列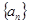 为等比数列,即可写出数列
为等比数列,即可写出数列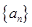 的通项公式为
的通项公式为 ,由数列
,由数列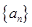 的通项公式及
的通项公式及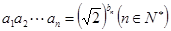 ,可得数列
,可得数列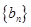 的通项公式为,
的通项公式为, ;(2)(i)求数列
;(2)(i)求数列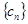 的前
的前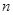 项和
项和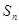 ,首先求数列
,首先求数列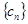 的通项公式,由
的通项公式,由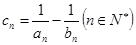 ,将
,将 ,
,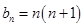 代入整理得
代入整理得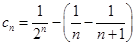 ,利用等比数列求和公式,即可得数列
,利用等比数列求和公式,即可得数列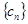 的前
的前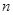 项和
项和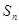 ;(ii)求正整数
;(ii)求正整数 ,使得对任意
,使得对任意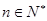 ,均有
,均有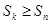 ,即求数列
,即求数列 的最大项,即求数列
的最大项,即求数列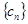 得正数项,由数列
得正数项,由数列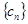 的通项公式,可判断出
的通项公式,可判断出 ,当
,当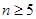 时,
时,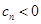 ,从而可得对任意
,从而可得对任意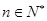 恒有
恒有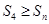 ,即
,即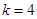 .
.
(1)由题意,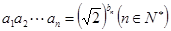 ,
,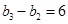 ,知
,知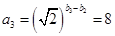 ,又有
,又有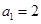 ,得公比
,得公比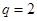 (
(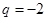 舍去),所以数列
舍去),所以数列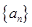 的通项公式为
的通项公式为 ,所以
,所以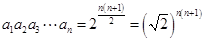 ,故数列
,故数列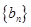 的通项公式为,
的通项公式为, ;
;
(2)(i)由(1)知,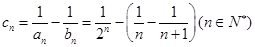 ,所以
,所以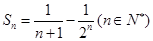 ;
;
(ii)因为 ;当
;当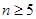 时,
时,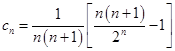 ,而
,而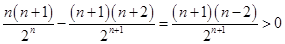 ,得
,得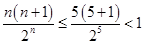 ,所以当
,所以当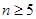 时,
时,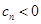 ,综上对任意
,综上对任意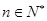 恒有
恒有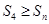 ,故
,故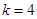 .
.
点评:本题主要考查等差数列与等比的列得概念,通项公式,求和公式,不等式性质等基础知识,同时考查运算求解能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 满足:
满足: ,
,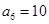 .
.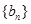 的各项均为正数,
的各项均为正数,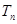 为其前
为其前 项和,若
项和,若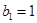 ,
,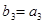 ,求
,求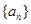 的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
的首项为23,公差为整数,且第6项为正数,从第7项起为负数。 是正数时,求n的最大值。
是正数时,求n的最大值。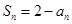 ,数列{bn}满足b1=1,b3+b7=18,且
,数列{bn}满足b1=1,b3+b7=18,且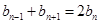 (n≥2).(1)求数列{an}和{bn}的通项公式;(2)若
(n≥2).(1)求数列{an}和{bn}的通项公式;(2)若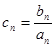 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.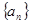 满足:
满足: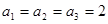 ,
,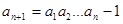 (
(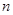 ≥3),记
≥3),记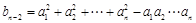
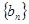 为等差数列,并求通项公式;
为等差数列,并求通项公式;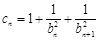 ,数列{
,数列{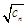 }的前n项和为
}的前n项和为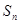 ,求证:
,求证: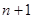 .
.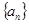 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示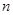 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 .
. +n-4.
+n-4.