题目内容
在等差数列{an}和等比数列{bn}中,a1=b1=1,b4=8,{an}的前10项和S10=55.
(1)求an和bn;
(2)现分别从{an}和{bn}的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值
相等的概率.
 ,
, ;(2)
;(2)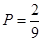
解析试题分析:(1)根据等差数列的首项和公差求通项公式;(2)根据等比数列的首项和公比求通项公式;注意题中限制条件;(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(4)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;
试题解析:解:(1)设{an}的公差为d,{bn}的公比为q.依题意得
S10=10+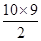 d=55,b4=q3=8, 2分
d=55,b4=q3=8, 2分
解得d=1,q=2, 4分
所以an=n,bn=2n-1. 6分
(2)分别从{an},{bn}的前3项中各随机抽取一项,得到的基本事件有9个:
(1,1),(1,2),(1,4),(2,1),(2,2),(2,4),(3,1),(3,2),(3,4). 8分
符合题意的基本事件有2个:(1,1),(2,2). 10分
故所求的概率P=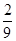 12分
12分
考点:(1)等差数列和等比数列的通项公式;(2)古典概型概率公式的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 }中,
}中, =14,前10项和
=14,前10项和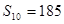 .
.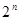 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前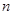 项和
项和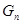 .
.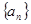 中,
中,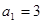 ,其前
,其前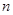 项和为
项和为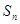 ,等比数列
,等比数列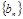 的各项均为正数,
的各项均为正数,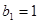 ,公比为
,公比为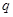 ,且
,且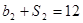 ,
,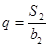 .
.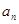 与
与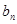 ; (2)设数列
; (2)设数列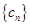 满足
满足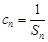 ,求
,求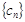 的前
的前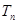 .
. 满足:
满足: ,
,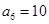 .
.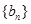 的各项均为正数,
的各项均为正数,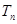 为其前
为其前 项和,若
项和,若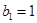 ,
,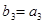 ,求
,求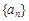 的前n项和为
的前n项和为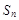 ,且
,且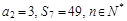
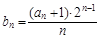 ,求数列
,求数列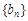 的前n项和Tn.
的前n项和Tn.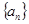 的首项
的首项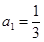 ,公比
,公比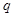 满足
满足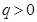 且
且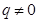 ,又已知
,又已知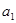 ,
, ,
,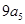 ,成等差数列;
,成等差数列; ,求
,求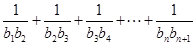 的值;
的值;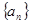 满足:
满足: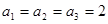 ,
,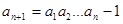 (
(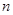 ≥3),记
≥3),记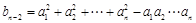
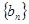 为等差数列,并求通项公式;
为等差数列,并求通项公式;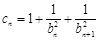 ,数列{
,数列{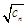 }的前n项和为
}的前n项和为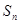 ,求证:
,求证: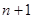 .
. 中,若
中,若 ,则
,则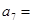
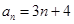 ,则数列{an}是公差为 的等差数列.
,则数列{an}是公差为 的等差数列.