题目内容
【题目】已知在数列{an}中,设a1为首项,其前n项和为Sn,若对任意的正整数m,n都有不等式S2m+S2n<2Sm+n(m≠n)恒成立,且2S6<S3.
(1)设数列{an}为等差数列,且公差为d,求![]() 的取值范围;
的取值范围;
(2)设数列{an}为等比数列,且公比为q(q>0且q≠1),求a1![]() q的取值范围.
q的取值范围.
【答案】(1)![]() <﹣3;(2)a1
<﹣3;(2)a1![]() q>0
q>0
【解析】
(1)根据已知条件,由于数列是等差数列,运用等差数列的求和公式,建立不等式,进一步求出相应的结果;
(2)根据已知条件,由于数列是等比数列,运用等比数列的求和公式,建立不等式,进一步求出相应的结果.
在数列{an}中,设a1为首项,其前n项和为Sn,
若对任意的正整数m、n都有不等式S2m+S2n<2Sm+n(m≠n)恒成立,
(1)设{an}为等差数列,且公差为d,
则:2ma1+![]() d+2na1+
d+2na1+![]() d<2[(m+n)a1+
d<2[(m+n)a1+![]() d],
d],
整理得:(m﹣n)2d<0,则d<0,由2S6>S3,整理得:9a1+27d>0,
则a1>﹣3d,所以d<0,![]() <﹣3;
<﹣3;
(2)设{an}为等比数列,且公比为q(q>0且q≠1),
则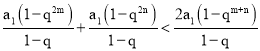 ,整理得
,整理得![]() (2qm+n﹣q2m﹣q2n)<0,
(2qm+n﹣q2m﹣q2n)<0,
则:﹣![]() (qm﹣qn)2<0,所以
(qm﹣qn)2<0,所以![]() >0,由2S6>S3,则:2q6﹣q3﹣1<0
>0,由2S6>S3,则:2q6﹣q3﹣1<0
解得:﹣![]() <q3<1,由于q>0,所以:0<q<1,则:a1>0.即有a1
<q3<1,由于q>0,所以:0<q<1,则:a1>0.即有a1![]() q>0.
q>0.

练习册系列答案
相关题目
