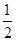题目内容
已知函数 (
( 是常数)在
是常数)在 处的切线方程为
处的切线方程为 ,且
,且 .
.
(1)求常数 的值;
的值;
(2)若函数 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围.
的取值范围.
 (
( 是常数)在
是常数)在 处的切线方程为
处的切线方程为 ,且
,且 .
.(1)求常数
 的值;
的值;(2)若函数
 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围.
的取值范围.(1)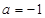 ,
,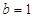 ,
,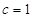 (2)
(2)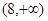
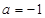 ,
,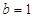 ,
,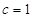 (2)
(2)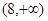
试题分析:(1)在
 处的切线切线斜率为
处的切线切线斜率为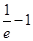 ,由导数的几何意义可知
,由导数的几何意义可知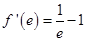 ,将
,将 代入切线方程可得
代入切线方程可得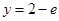 即
即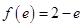 又因为
又因为 ,解以上三个方程组成的方程组可得
,解以上三个方程组成的方程组可得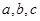 的值。(2)由(1)可知函数
的值。(2)由(1)可知函数 的解析式,从而可得函数
的解析式,从而可得函数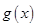 解析式。将其求导可得
解析式。将其求导可得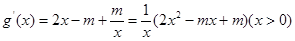 ,令
,令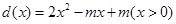 ,可将问题转化为函数
,可将问题转化为函数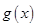 在
在 内有极值,即
内有极值,即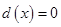 应有2个根(判别式应大于0),但在
应有2个根(判别式应大于0),但在 内至少有一个根(故应分两种情况讨论)。因为
内至少有一个根(故应分两种情况讨论)。因为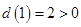 ,所以
,所以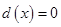 在
在 内有一个根时应有
内有一个根时应有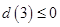 ,
,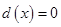 在
在 内有两个根时应因为
内有两个根时应因为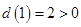 ,则
,则 且顶点纵坐标小于0
且顶点纵坐标小于0(1)由题设知,
 的定义域为
的定义域为 ,
,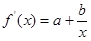 ,
,因为
 在
在 处的切线方程为
处的切线方程为 ,
,所以
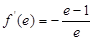 ,且
,且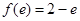 ,即
,即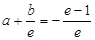 ,且
,且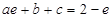 ,
,又
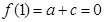 ,解得
,解得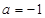 ,
,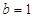 ,
,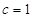
(2)由(Ⅰ)知

因此,
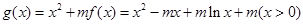
所以
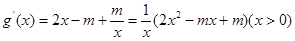
令
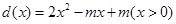 .
.(ⅰ)当函数
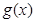 在
在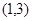 内有一个极值时,
内有一个极值时,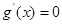 在
在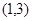 内有且仅有一个根,即
内有且仅有一个根,即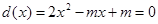 在
在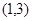 内有且仅有一个根,又因为
内有且仅有一个根,又因为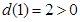 ,当
,当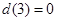 ,即
,即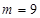 时,
时,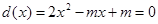 在
在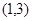 内有且仅有一个根
内有且仅有一个根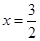 ,当
,当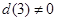 时,应有
时,应有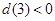 ,即
,即 ,解得
,解得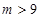 ,所以有
,所以有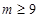 .
.(ⅱ)当函数
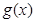 在
在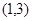 内有两个极值时,
内有两个极值时,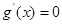 在
在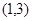 内有两个根,即二次函数
内有两个根,即二次函数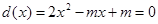 在
在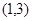 内有两个不等根,
内有两个不等根,所以
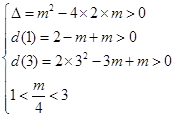 ,解得
,解得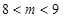 .
. 综上,实数
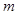 的取值范围是
的取值范围是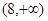

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
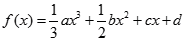 的图像过原点,且在点
的图像过原点,且在点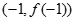 处的切线与
处的切线与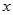 轴平行,对任意
轴平行,对任意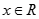 ,都有
,都有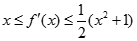 .
.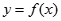 在点
在点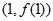 处切线的斜率;
处切线的斜率;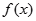 的解析式;
的解析式;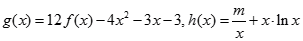 ,对任意
,对任意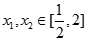 ,都有
,都有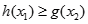 .求实数
.求实数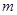 的取值范围.
的取值范围. 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( ) 时取得极值,则
时取得极值,则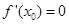
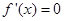 ,则
,则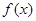 在
在 -x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
-x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )



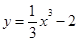 在点
在点 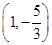 处切线的斜率为( )
处切线的斜率为( )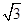

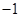
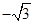
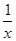 与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )