题目内容
18.在△ABC中,若sinC+sin(B-A)=sin2A,则△ABC的形状为( )| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
分析 由两角和与差的三角函数公式结合三角形的知识可得cosA=0或sinA=sinB.进而可作出判断.
解答 解:∵sinC+sin(B-A)=sin2A,
∴sin(A+B)+sin(B-A)=sin2A.
∴sinAcosB+cosAsinB+sinBcosA-cosBsinA=2sinAcosA
∴2sinBcosA=2sinAcosA.
∴cosA(sinA-sinB)=0,
∴cosA=0或sinA=sinB.
∵0<A,B<π,∴A=$\frac{π}{2}$或A=B.
∴△ABC为直角三角形或等腰三角形.
故选:D.
点评 本题考查三角形形状的判断,涉及两角和与差的三角函数公式,属基础题.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
8.下列四个选项中错误的是( )
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0则x=1”. | |
| B. | 若p∧q为真命题,则p∨q为真命题. | |
| C. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0. | |
| D. | “x>2”是“x2-3x+2>0”成立的必要不充分条件. |
8.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1、F2,已知线段F1F2被点(b,0)分成3:1的两段,则此双曲线的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
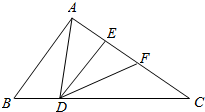 △ABC中D是BC边上的一个四等分点,AE:EF:FC=2;2:3,已知△DEF的面积为12cm2,那么△ABC的面积是多少?
△ABC中D是BC边上的一个四等分点,AE:EF:FC=2;2:3,已知△DEF的面积为12cm2,那么△ABC的面积是多少?