题目内容
3.在平面直角坐标系xoy中,圆C的参数方程为$\left\{\begin{array}{l}x=1+2cost\\ y=-\sqrt{3}+2sint\end{array}\right.$(t为参数).在极坐标系(与平面直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,直线l的方程为$2ρsin(θ-\frac{π}{6})=m(m∈R)$.(Ⅰ)求圆C的普通方程及直线l的直角坐标方程;
(Ⅱ)设直线l被圆C截得的弦长为$2\sqrt{3}$,求m的值.
分析 (Ⅰ)把圆的参数方程变形,平方后相加可得圆的普通方程,把$2ρsin(θ-\frac{π}{6})=m(m∈R)$左边展开两角差的正弦,代入x=ρcosθ,y=ρsinθ得答案;
(Ⅱ)由直线l被圆C截得的弦长为$2\sqrt{3}$,圆的半径为2,可得圆心到直线的距离,由点到直线的距离公式求得m的值.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}x=1+2cost\\ y=-\sqrt{3}+2sint\end{array}\right.$,得$\left\{\begin{array}{l}{x-1=2cost}\\{y+\sqrt{3}=2sint}\end{array}\right.$,两式平方相加得:${(x-1)^2}+{(y+\sqrt{3})^2}=4$,
∴圆C的普通方程为${(x-1)^2}+{(y+\sqrt{3})^2}=4$;
由$2ρsin(θ-\frac{π}{6})=m⇒2ρsinθ•\frac{{\sqrt{3}}}{2}-2ρcosθ•\frac{1}{2}=m$,
从而得$\sqrt{3}ρsinθ-ρcosθ=m$,∴$x-\sqrt{3}y+m=0$;
(Ⅱ)∵直线l被圆C截得的弦长为$2\sqrt{3}$,且圆的半径为2,
∴圆心到直线的距离为1,
即$\frac{{|1-\sqrt{3}×(-\sqrt{3})+m|}}{2}=1$,
从而得|m+4|=2,解得m=-2或-6.
点评 本题考查参数方程化普通方程,考查了极坐标方程化直角坐标方程,考查弦心距、弦长及圆的半径间的关系的运用,是中档题.

练习册系列答案
相关题目
18.在△ABC中,若sinC+sin(B-A)=sin2A,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
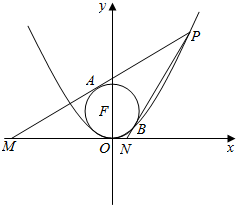 (文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.
(文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B. 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD且BC=$\frac{1}{2}$AD,BE∥AF且BE=$\frac{1}{2}$AF,G,H分别为FA,FD的中点.证明:四边形BCHG是平行四边形.
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD且BC=$\frac{1}{2}$AD,BE∥AF且BE=$\frac{1}{2}$AF,G,H分别为FA,FD的中点.证明:四边形BCHG是平行四边形.