题目内容
7.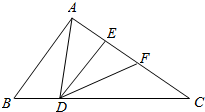 △ABC中D是BC边上的一个四等分点,AE:EF:FC=2;2:3,已知△DEF的面积为12cm2,那么△ABC的面积是多少?
△ABC中D是BC边上的一个四等分点,AE:EF:FC=2;2:3,已知△DEF的面积为12cm2,那么△ABC的面积是多少?
分析 根据等底同高的三角形面积相等,可得△ABC的面积是△ADC的面积的$\frac{4}{3}$倍,△ADC的面积又是△DEF的面积的$\frac{7}{2}$倍,进而得到答案.
解答 解:∵AE:EF:FC=2;2:3,△DEF的面积为12cm2,
∴△ADC的面积为$\frac{2+2+3}{2}$×12=42cm2,
又∵D是BC边上的一个四等分点,
∴△ABC的面积S=42×$\frac{4}{3}$=56cm2
点评 本题考查的知识点是三角形面积的求法,正确理解阴影部分面积是由哪几部分割(补)而成的,是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
18.在△ABC中,若sinC+sin(B-A)=sin2A,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰三角形或直角三角形 |
2.已知映射f:A→B,其中A=B=R,对应法则f:x→y=$\left\{{\begin{array}{l}{{x^2}-2x,x≥0}\\{-{x^2}-2x,x<0}\end{array}}$,实数k∈B,且k在集合A中只有一个原象,则k的取值范围是( )
| A. | (-∞,-1]∪[1,+∞) | B. | (-∞,-1)∪(1,+∞) | C. | (-1,1) | D. | [-1,1] |