Question

【题目】已知椭圆的右焦点为，右准线为.过点作与坐标轴都不垂直的直线与椭圆交于，两点，线段的中点为，为坐标原点，且直线与右准线交于点.

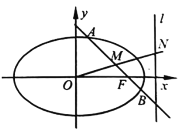
（1）求椭圆的标准方程；

（2）若，求直线的方程；

（3）是否存在实数，使得恒成立？若存在，求实数的值；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）；（3）存在，且.

【解析】

（1）根据准线的定义得，又由，结合可求得，得椭圆标准方程；

（2）由可求得点横坐标，设直线方程为，代入椭圆方程整理后应用韦达定理得，由可得，得直线方程；

（3）设，得，由点差法可得，从而得，则可得点坐标，然后计算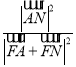可得．

（1）由已知可得： ，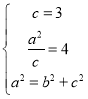

解得：

椭圆的标准方程为：.

（2）由可知：

即，可得：，

设，直线AB的方程为，

联立 ，得：，

为线段的中点，则，

即，解得：，

所以直线的方程为.

（3）设，，，，，，

由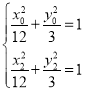，两方程相减得，即，

∴，即，

又，∴，∵，∴，即，

，，，

，

，

∴．

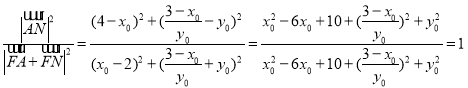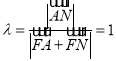∴存在满足题意的，且．