题目内容
已知P是△ABC所在平面内任意一点,且
+
+
=3
,则G是△ABC的( )
| PA |
| PB |
| PC |
| PG |
| A.外心 | B.内心 | C.重心 | D.垂心 |
由
+
+
=3
?(
-
)+(
-
)+(
-
)-3
=
?
+
+
=
由题意画出简图为:
由于
+
+
=
?
+
=
,
在图形中,利用平行四边行法则及两向量的加法原理可知:GB为两相邻边的平行四边形的对角线GD,
由于四边形GADB为平行四边形,所以GD平分AB,所以点G在三角形ABC的边AB的中线上,
同理点G应该在BC边的中线上,利用重心的定义可知G是△ABC重心(即三条边上中线的交点).
故选C.

| PA |
| PB |
| PC |
| PG |
| GA |
| GP |
| GB |
| GP |
| GC |
| GP |
| GP |
| 0 |
| GA |
| GB |
| GC |
| 0 |
由题意画出简图为:
由于
| GA |
| GB |
| GC |
| 0 |
| GA |
| GB |
| CG |
在图形中,利用平行四边行法则及两向量的加法原理可知:GB为两相邻边的平行四边形的对角线GD,
由于四边形GADB为平行四边形,所以GD平分AB,所以点G在三角形ABC的边AB的中线上,
同理点G应该在BC边的中线上,利用重心的定义可知G是△ABC重心(即三条边上中线的交点).
故选C.


练习册系列答案
相关题目
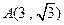 ,O为坐标原点,点
,O为坐标原点,点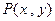 的坐标x,y满足
的坐标x,y满足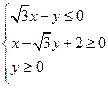 ,则向量
,则向量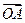 在向量
在向量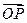 方向上的投影的取值范围是( )
方向上的投影的取值范围是( )



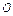 为
为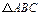 内一点,且
内一点,且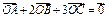 ,则
,则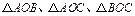 的面积之比等于
的面积之比等于
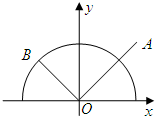

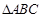 中,
中,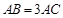 ,
,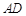 是
是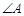 的平分线,且
的平分线,且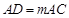 ,则实数
,则实数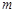 的取值范围是 ▲ .
的取值范围是 ▲ .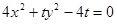 的虚轴长等于( )
的虚轴长等于( ) 

