题目内容
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求满足
,求满足![]() 的所有正整数
的所有正整数![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 的值为1与2.
的值为1与2.
【解析】
(Ⅰ)由条件可得,![]() ,再用累加法求解即可;
,再用累加法求解即可;
(Ⅱ)利用分类讨论法求和或错位相减法求解.
(Ⅱ)(解法一)由题意得![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,令
,令![]() ,其前
,其前![]() 项和为
项和为![]() ,由此讨论可求出答案.
,由此讨论可求出答案.
(解法二)令![]() ,利用错位相减法求得其前
,利用错位相减法求得其前![]() 项和
项和![]() ,从而求出
,从而求出![]() ,记
,记![]()
![]() ,由此讨论即可求出答案.
,由此讨论即可求出答案.
解:(Ⅰ)![]() ,
,
![]() ,即
,即![]() ,
,
由累加法,当![]() 时,
时,
![]() ,
,
代入![]() 得,
得,
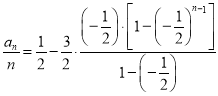
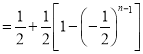
![]() ,
,
![]() (
(![]() ),
),
![]() 也满足上式,
也满足上式,
∴![]() ;
;
(Ⅱ)解法一:![]() ,
,
数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
令![]() ,
,
其前![]() 项和为
项和为![]() ,
,
则有![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]()
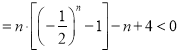 ,则有
,则有![]() ,
,
综上,不等式成立的![]() 的值为1与2.
的值为1与2.
解法二:令![]() ,设其前
,设其前![]() 项和为
项和为![]() ,
,
∴![]() ,
,
∴![]() ,
,
两式相减得,![]()
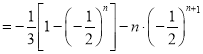
![]() ,
,
![]() ,
,
则有![]() ,
,
记![]()
![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 且
且![]() 为奇数时,
为奇数时,![]() ,
,![]() ,则
,则![]() ;
;
当![]() 且
且![]() 为偶数时,
为偶数时,![]() ,
,![]() ,则
,则![]() ;
;
综上所述,不等式成立的![]() 的值为1与2.
的值为1与2.

练习册系列答案
相关题目