Question

18．已知函数y=1+2sinx．
（1）用五点作图法作出函数在x∈[0，2π]间的图象；
（2）若x∈R，①试根据函数图象写出函数的单调减区间；
②当x取何值时，y取最大值．

Answer 1

分析 （1）用五点作图法作出f（x）在一个周期内的图象；
（2）根据三角函数的图象即可求f（x） 函数的单调减区间或最大值．

解答 解：列表为

x	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
sinx	0	1	0	-1	0
y=1+2sinx	1	3	1	-1	1

画出图形：
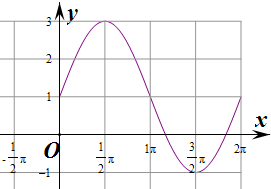
（2）由图象知函数的单调减区间为[2kπ+$\frac{π}{2}$，2kπ+$\frac{3π}{2}$]，k∈Z，
当x=2kπ+$\frac{π}{2}$，k∈Z，函数取得最大值为3．

点评 本题考查的知识点是五点法作函数y=Asin（ωx+φ）的图象，其中描出五个关键点的坐标是解答本题的关键．