题目内容
【题目】等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P﹣AE﹣C为120°,设点P在面ABE上的射影为H. 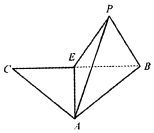
(1)证明:点H为EB的中点;
(2)若 ![]() ,求直线BE与平面ABP所成角的正弦值.
,求直线BE与平面ABP所成角的正弦值.
【答案】
(1)证明:依题意,AE⊥BC,则AE⊥EB,AE⊥EP,EB∩EP=E.
∴AE⊥面EPB.
故∠CEP为二面角C﹣AE﹣P的平面角,则点P在面ABE上的射影H在EB上.
由∠CEP=120°得∠PEB=60°.
∴EH= ![]() EP=
EP= ![]() .
.
∴H为EB的中点.
(2)解:过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,
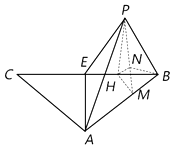
则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,
∴HN⊥面PAB.故HB在面PAB上的射影为NB.
∴∠HBN为直线BE与面ABP所成的角.
依题意,BE= ![]() BC=2,BH=
BC=2,BH= ![]() BE=1.
BE=1.
在△HMB中,HM= ![]() ,
,
在△EPB中,PH= ![]() ,
,
∴在Rt△PHM中,HN= ![]() .
.
∴sin∠HBN= ![]() .
.
【解析】(1)证明:∠CEP为二面角C﹣AE﹣P的平面角,则点P在面ABE上的射影H在EB上,即可证明点H为EB的中点;(2)过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,HN⊥面PAB.故HB在面PAB上的射影为NB,∠HBN为直线BE与面ABP所成的角,即可求直线BE与平面ABP所成角的正弦值.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则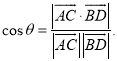 .
.

练习册系列答案
相关题目
