题目内容
【题目】如图正方体![]() 的棱长为
的棱长为![]() ,
,![]() 、
、![]() 、
、![]() ,分别为
,分别为![]() 、
、![]() 、
、![]() 的中点.则下列命题:①直线
的中点.则下列命题:①直线![]() 与平面
与平面![]() 平行;②直线
平行;②直线![]() 与直线
与直线![]() 垂直;③平面
垂直;③平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() ;④点
;④点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等;⑤平面
的距离相等;⑤平面![]() 截正方体所得两个几何体的体积比为
截正方体所得两个几何体的体积比为![]() .其中正确命题的序号为_______.
.其中正确命题的序号为_______.
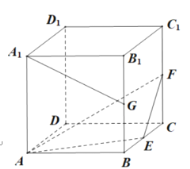
【答案】①③⑤
【解析】
连结![]() ,由
,由![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() ∥
∥![]() ,所以
,所以![]() 四点共面,截面图形为等腰梯形,然后对各个命题进行逐一判断.
四点共面,截面图形为等腰梯形,然后对各个命题进行逐一判断.
连结![]() ,由
,由![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
则![]() ∥
∥![]() ,又
,又![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]() 且
且![]() =
=![]() .
.
所以截面四边形形![]() 为等腰梯形.
为等腰梯形.
对①, ![]() 、
、![]() ,分别为
,分别为![]() 、
、![]() 的中点,
的中点,
所以![]() ∥
∥![]() ,且
,且![]() =
=![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
所以![]() ∥
∥![]() ,所以
,所以![]() ∥平面
∥平面![]() ,故①正确.
,故①正确.
对②, ![]() ∥
∥![]() ,在
,在![]() 中,
中,![]() ,
,
显然![]() 与
与![]() 不垂直,则直线
不垂直,则直线![]() 与直线
与直线![]() 不垂直,故②不正确.
不垂直,故②不正确.
对③, 平面![]() 截正方体所得的截面为四边形
截正方体所得的截面为四边形![]() ,
,
又四边形![]() 为等腰梯形,其中
为等腰梯形,其中![]() ,
,![]() ,
,
梯形![]() 的高为
的高为![]() ,
,
则其面积为![]() .故③正确.
.故③正确.
对④,点![]() 是
是![]() 的中点,所以
的中点,所以![]() 到面
到面![]() 的距离相等.
的距离相等.

![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,延长
的中点,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
即直线![]() 交平面
交平面![]() 于点
于点![]() ,则
,则![]() 为
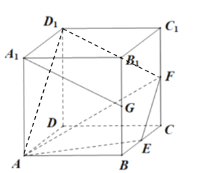
为![]() 的中点,如图,
的中点,如图,
分别过![]() 作平面
作平面![]() 的垂线,垂足分为
的垂线,垂足分为![]() ,
,
所以![]() 分别为点
分别为点![]() 到面
到面![]() 的距离,则三点
的距离,则三点![]() 共线,
共线,
根据三角形的相似可得:![]() ,所以
,所以![]() 到面
到面![]() 的距离不相等,
的距离不相等,
则点![]() 与点
与点![]() 到平面
到平面![]() 的距离不相等,故④不正确.
的距离不相等,故④不正确.
对⑤, 由条件可知多面体![]() 为棱台,
为棱台,
其体积为![]() ,
,
平面![]() 截正方体所得两个几何体的体积比为
截正方体所得两个几何体的体积比为 ,故⑤正确.
,故⑤正确.
故答案为:①③⑤.

 名校课堂系列答案
名校课堂系列答案【题目】国家学生体质健康测试专家组到某学校进行测试抽查,在高三年级随机抽取100名男生参加实心球投掷测试,测得实心球投掷距离(均在5至15米之内)的频数分布表如下(单位:米):
分组 |
|
|
|
|
|
频数 | 9 | 23 | 40 | 22 | 6 |
规定:实心球投掷距离在![]() 之内时,测试成绩为“良好”,以各组数据的中间值代表这组数据的平均值
之内时,测试成绩为“良好”,以各组数据的中间值代表这组数据的平均值![]() ,将频率视为概率.
,将频率视为概率.
(1)求![]() ,并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
,并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
(2)现在从实心球投掷距离在![]() ,
,![]() 之内的男生中用分层抽样的方法抽取5人,再从这5人中随机抽取3人参加提高体能的训练,求:在被抽取的3人中恰有两人的实心球投掷距离在
之内的男生中用分层抽样的方法抽取5人,再从这5人中随机抽取3人参加提高体能的训练,求:在被抽取的3人中恰有两人的实心球投掷距离在![]() 内的概率.
内的概率.