题目内容
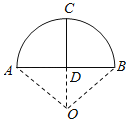
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的正方形
,该纸片上的正方形![]() 的中心为
的中心为![]() 为圆
为圆![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,
,![]() 使得
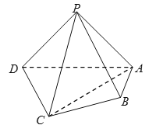
使得![]() 重合,得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为__________.
重合,得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为__________.

【答案】![]()
【解析】
先连接![]() 交
交![]() 与点
与点![]() ,结合四棱锥的侧面积是底面积的2倍,求得正方形边长,再画出折叠后的立体图形,找出外接球的球心,结合勾股定理即可求解
,结合四棱锥的侧面积是底面积的2倍,求得正方形边长,再画出折叠后的立体图形,找出外接球的球心,结合勾股定理即可求解
如图:

连接![]() 交
交![]() 与点
与点![]() ,设正方形边长为
,设正方形边长为![]() ,
,![]() ,则
,则![]() ,
,![]()
则正方形面积为:![]() ,四棱锥的侧面积为:
,四棱锥的侧面积为:![]() ,由题意得
,由题意得![]() ,即
,即![]() ,解得
,解得![]() ,画出折叠后的立体图形.如图:
,画出折叠后的立体图形.如图:

设重合点为![]() ,该四棱锥为正四棱锥,球心应在
,该四棱锥为正四棱锥,球心应在![]() 的连线上,设为
的连线上,设为![]() ,设外接球半径为
,设外接球半径为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() ,即
,即![]() ,解得
,解得![]() ,外接球表面积为:
,外接球表面积为:![]()
故答案为![]()

练习册系列答案
相关题目