题目内容
12. 设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.(Ⅰ)若$\overrightarrow{ED}$=6$\overrightarrow{DF}$,求k的值;
(Ⅱ)求四边形AEBF面积的最大值.
分析 (1)依题可得椭圆的方程,设直线AB,EF的方程分别为x+2y=2,y=kx,D(x0,kx0),E(x1,kx1),F(x2,kx2),且x1,x2满足方程,进而求得x2的表达式,进而根据$\overrightarrow{ED}$=6$\overrightarrow{DF}$,求得x0的表达式,由D在AB上知x0+2kx0=2,进而求得x0的另一个表达式,两个表达式相等求得k.
(Ⅱ)由题设可知|BO|和|AO|的值,设y1=kx1,y2=kx2,进而可表示出四边形AEBF的面积进而根据基本不等式的性质求得最大值.
解答 解:(Ⅰ)依题设得椭圆得a=4,b=2方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$
直线AB,EF的方程分别为x+2y=4,y=kx(k>0)
设D(x0,kx0),E(x2,kx2)其中x1<x2
且x1,x2满足方程(1+4k2)x2=16.故x2=-x1=$\frac{4}{\sqrt{1+4{k}^{2}}}①$
由$\overrightarrow{ED}=6\overrightarrow{DF}$知x0-x1=6(x2-x0),得x0=$\frac{1}{7}(6{x}_{2}+{x}_{1})=\frac{5}{7}{x}_{2}=\frac{20}{7\sqrt{1+4{k}^{2}}}$
由D在AB上知x0+2kx0=4,得x0=$\frac{4}{1+2{k}^{2}}$
所以$\frac{4}{1+2k}=\frac{20}{7\sqrt{1+4{k}^{2}}}$,化简得k=$\frac{2}{3}$或k=$\frac{3}{8}$
(Ⅱ)根据点到直线得距离公式和①式知,点E,F到AB的距离分别为
${k}_{1}=\frac{|{x}_{1}+2k{x}_{1}-4|}{\sqrt{5}}=\frac{4(1+2k+\sqrt{1+4{k}^{2}})}{\sqrt{5}(1+4{k}^{2})}$,${k}_{2}=\frac{|{x}_{2}+2k{x}_{2}-4|}{\sqrt{5}}=\frac{4(1+2k-\sqrt{1+4{k}^{2}})}{\sqrt{5}\sqrt{1+4{k}^{2}}}$
又|AB|=2$\sqrt{5}$,所以四边形AEBF的面积为S=$\frac{1}{2}|AB|({k}_{1}+{k}_{2})=\frac{1}{2}×2\sqrt{5}\frac{8(1+2k)}{\sqrt{5(1+4{k}^{2})}}$=$8\sqrt{\frac{1+4{k}^{2}-4k}{1+4{k}^{2}}}$
=4$\sqrt{1+\frac{4k}{1+4{k}^{2}}}≤8\sqrt{2}$
当2k=1,即当k=$\frac{1}{2}$时,上式取等号,所以S的最大值为8$\sqrt{2}$
点评 本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容,问题的解决具有入口宽、方法灵活多样等,而不同的解题途径其运算量繁简差别很大.

| A. | $\sqrt{10}$ | B. | 5 | C. | 3 | D. | $\sqrt{11}$ |
| A. | 若{dn}满足dn=$\frac{{{b_1}+2{b_2}+3{b_3}+…+n{b_n}}}{1+2+3+…n}$,则{dn}也是等比数列 | |
| B. | 若{dn}满足dn=$\frac{{{b_1}•2{b_2}•3{b_3}•…•n{b_n}}}{1•2•3•…•n}$,则{dn}也是等比数列 | |
| C. | 若{dn}满足${d_n}={[{b_1}•(2{b_2})•(3{b_3})•…•(n{b_n})]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 | |
| D. | 若{dn}满足${d_n}={[{b_1}•{b_2}^2•{b_3}^3•…•{b_n}^n]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 |
 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求三棱锥N-A1BC的体积.
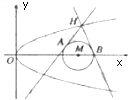 如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.
如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.