题目内容
17.求x2+y2-4y-6=0与x2+y2-5x+y-6=0的交点.分析 由x2+y2-4y-6=0与x2+y2-5x+y-6=0,相减可得y=x,代入x2+y2-4y-6=0,可得x2-2x-3=0,即可求出x2+y2-4y-6=0与x2+y2-5x+y-6=0的交点.
解答 解:由x2+y2-4y-6=0与x2+y2-5x+y-6=0,相减可得y=x,
代入x2+y2-4y-6=0,可得x2-2x-3=0,
∴x=-1或3,
∴交点坐标为(-1,-1),(3,3).
点评 本题考查圆与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
7.复数$\frac{1-7i}{1+i}$的虚部为( )
| A. | 4i | B. | -4i | C. | 4 | D. | -4 |
12.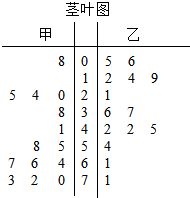 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )
 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )| A. | 55,36 | B. | 55.5,36.5 | C. | 56.5,36.5 | D. | 58,37 |
2.等差数列{an}中,a7=12,a6=10,则该数列的通项公式为( )
| A. | an=3n-8 | B. | an=2n-2 | C. | an=2n+2 | D. | an=2n-1 |
7.设复数z1=2-i,z2=1-3i,则复数$\frac{i}{{z}_{1}}$+$\frac{\overline{{z}_{2}}}{5}$的虚部等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 如图,在△ABC中,C=$\frac{π}{2}$,A=$\frac{π}{3}$,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,若DE的长为2,则AC=10.
如图,在△ABC中,C=$\frac{π}{2}$,A=$\frac{π}{3}$,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,若DE的长为2,则AC=10.