Question

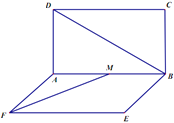
【题目】如图，在四棱锥中， 底面， ， ， ， 为棱的中点．

（）求证： ．

（）求证：平面平面．

（）试判断与平面是否平行？并说明理由．

Answer 1

【答案】（1）见解析；（2）见解析（3）见解析.

【解析】试题分析：（1）PD⊥底面ABCD，DC底面ABCDPD⊥DC．又AD⊥DC，AD∩PD=D故CD⊥平面PAD．又AE平面PAD，得CD⊥AE．
（2）由AB∥DC，CD⊥平面PAD，AB⊥平面PAD．又由AB平面PAB，得平面PAB⊥平面PAD．
（3）PB与平面AEC不平行．假设PB∥平面AEC，由已知得到，这与矛盾.

试题解析：

（）证明：∵底面， 底面，

∴，

又， ，

∴平面，

∵平面，

∴．

（）证明： ， 平面，

∴平面，

又平面，

∴平面平面．

（）与平面不平行，

假设平面，设，

连结，则平面平面，

又平面，

∴，

∴在中有，

由是中点可得，即，

∵，

∴，这与矛盾，

所以假设不成立，即与平面不平行．