Question

【题目】给出下列四个命题：

①命题“x∈R，cosx>0”的否定是“x0∈R，cosx0≤0”；

②若0<a<1，则函数f(x)＝x2＋ax－3只有一个零点；

③函数y＝2sinxcosx在上是单调递减函数；

④若lga＋lgb＝lg(a＋b)，则a＋b的最小值为4.

其中真命题的序号是________．

Answer 1

【答案】①④

【解析】由全称命题的否定是特称命题知①为真命题．

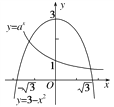
在同一直角坐标系内作出y＝3－x2，y＝ax(0<a<1)的图象如图所示．由图知两函数图象有两个交点，则函数f(x)＝x2＋ax－3有两个零点，故②为假命题．

由y＝2sinxcosx＝sin2x，

又时， ，

故y＝2sinxcosx在上是增函数，因此③为假命题．

④中由lga＋lgb＝lg(a＋b)知，

ab＝a＋b且a>0，b>0.

又，

所以令a＋b＝t(t>0)，

则4t≤t2，即t≥4，因此④为真命题．

故答案为：①④．