题目内容
【题目】已知实数
满足约束条件：
．
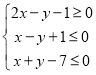（1）请画出可行域，并求
的最小值；
（2）若
取最大值的最优解有无穷多个，求实数
的值.
【答案】（1）可行域见解析，
；（2）
.
【解析】
试题分析：(1)先根据约束条件画出可行域,
,利用
的几何意义求最值,只需求出何时可行域内的点与点
连线的斜率的值最小,从而得到
的最小值；（2）先根据约束条件画出可行域,设
,再利用
的几何意义求最值,只需求出直线与可行域的边界
平行时,最优解有无穷多个,从而得到
值即可.
试题解析：解：（1）如图求画出可行域：．．．．．．．．．．．．．．．．． 2分
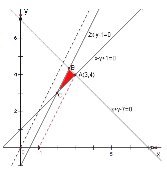
∵表示
与
连线的斜率，如图示，
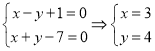，即
，
∴当
时，
．．．．．．．．．．．．．．．．．．．．．．6分
（2）取
得直线
，
∵当取得最值的最优解有无穷多个时，直线
与可行域边界所在直线平行，如图所示，当
，即
时，
取最小值的最优解有无穷多个，不合题意，．．．．．．．．．．．．．． 8分
当
，即
时，
取最大值的最优解有无穷多个，符合题意．．．．．．．．．．．．．．．10分
当
，即
时，
取最大值的最优解有无穷多个，符合题意．
综上得，．．．．．．．．．．．．．．．．．．．．．．．12分
练习册系列答案
相关题目
