题目内容
【题目】在直角坐标系![]() 中,点
中,点![]() 到两点
到两点![]() ,
,![]() 的距离之和等于4,设点
的距离之和等于4,设点![]() 的轨迹为
的轨迹为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,
两点,
(1)写出![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由题中条件:“点![]() 到两点
到两点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,”结合椭圆的定义知其轨迹式样,从而求得其方程;(2)先将直线方程与椭圆方程联立方程组,消去
,”结合椭圆的定义知其轨迹式样,从而求得其方程;(2)先将直线方程与椭圆方程联立方程组,消去![]() 得到一个一元二次方程,再利用根与系数的关系结合向量垂直的条件列关于
得到一个一元二次方程,再利用根与系数的关系结合向量垂直的条件列关于![]() 方程式即可求得参数
方程式即可求得参数![]() 值.
值.
试题解析:(1)设P(x,y),由椭圆定义可知,点P的轨迹C是以(0,-![]() )、(0,
)、(0,![]() )为焦点,长半轴为2的椭圆,它的短半轴
)为焦点,长半轴为2的椭圆,它的短半轴![]() ,
,
故曲线C的方程为![]() .
.
(2)设A(x1,y1),B(x2,y2),
联立方程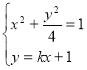
消去y并整理得(k2+4)x2+2kx-3=0.
其中Δ=4k2+12(k2+4)>0恒成立.
故![]()
![]() ,
,![]() .
.
若![]() ,即x1x2+y1y2=0.
,即x1x2+y1y2=0.
而y1y2=k2x1x2+k(x1+x2)+1,
于是x1x2+y1y2=-![]()
![]() ,
,
化简得-4k2+1=0,所以k=±![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目